
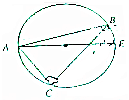
 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$. 分析 连BE,CE 推出tan∠ABCtan∠ACB=$\frac{AC}{BE}×\frac{AB}{CE}$,利用三角形相似证明tanB*tanC=$\frac{AD}{DE}$.
解答  证明:连BE,CE 因为∠ABC=∠AEC,
证明:连BE,CE 因为∠ABC=∠AEC,
所以tan∠ABC=tan∠AEC=$\frac{AC}{CE}$,
同理,tan∠ACB=tan∠AEB=$\frac{AB}{BE}$,
所以tan∠ABCtan∠ACB=tan∠AECtan∠AEB=$\frac{AC}{CE}×\frac{AB}{BE}$=$\frac{AC}{BE}×\frac{AB}{CE}$,
因为在圆中△ACD∽△BED,得,$\frac{AD}{BD}=\frac{AC}{BE}$,
同理△ABD∽△CED 所以$\frac{BD}{ED}=\frac{AB}{CE}$,
所以$\frac{AC}{BE}×\frac{AB}{CE}$=$\frac{AD}{BD}×\frac{BD}{ED}=\frac{AD}{ED}$,
即tanB*tanC=$\frac{AD}{DE}$.
点评 本题考查三角形的相似的判断与应用,考查逻辑推理能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,1) | C. | [$\frac{1}{2}$,1) | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:?x0∈R,使得x02-x0+1<0,则¬p:?x∈R,都有x2-x+1≥0. | |
| B. | 存在无数个α、β∈R,使得等式sin(α-β)=sinαcosβ+cosαsinβ成立 | |
| C. | 命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题是真命题 | |
| D. | “p∧q为真”是“p∨q为真”的必要不充分条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com