
【题目】已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|< ![]() )的最小正周期为2 π,最小值为﹣2,且当x=
)的最小正周期为2 π,最小值为﹣2,且当x= ![]() 时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
时,函数取得最大值4. (Ⅰ)求函数 f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间;
(Ⅲ)若当x∈[ ![]() ,
, ![]() ]时,方程f(x)=m+1有解,求实数m的取值范围.
]时,方程f(x)=m+1有解,求实数m的取值范围.
【答案】解:(Ⅰ)因为f(x)的最小正周期为2π, 得ω= ![]() =1,
=1,
又 ![]() ,解得
,解得 ![]() ,
,
由题意, ![]() +φ=2kπ+
+φ=2kπ+ ![]() (k∈Z),
(k∈Z),
即φ=2kπ﹣ ![]() (k∈Z),因为|φ|<
(k∈Z),因为|φ|< ![]() ,
,
所以,φ=﹣ ![]() ,
,
所以f(x)=3sin(x﹣ ![]() )+1
)+1
(Ⅱ)当2kπ- ![]() ≤x﹣
≤x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z),
(k∈Z),
即x∈[2kπ- ![]() ,2kπ+
,2kπ+ ![]() ](k∈Z)时,函数f(x)单调递增
](k∈Z)时,函数f(x)单调递增
(Ⅲ)方程f(x)=m+1可化为m=3sin(x﹣ ![]() )
)
因为x∈[ ![]() ,
, ![]() ],所以x﹣
],所以x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
由正弦函数图象可知,实数m的取值范围是[﹣ ![]() ,3]
,3]
【解析】(Ⅰ)由最小正周期可求ω,又 ![]() ,解得
,解得 ![]() ,由题意,
,由题意, ![]() +φ=2kπ+
+φ=2kπ+ ![]() (k∈Z),|φ|<
(k∈Z),|φ|< ![]() ,可解得φ,即可求得函数 f(x)的解析式;(Ⅱ)由2kπ-
,可解得φ,即可求得函数 f(x)的解析式;(Ⅱ)由2kπ- ![]() ≤x﹣
≤x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() (k∈Z)可求得函数f(x)的单调递增区间;(Ⅲ)方程f(x)=m+1可化为m=3sin(x﹣
(k∈Z)可求得函数f(x)的单调递增区间;(Ⅲ)方程f(x)=m+1可化为m=3sin(x﹣ ![]() ),由x∈[
),由x∈[ ![]() ,
, ![]() ],由正弦函数图象可解得实数m的取值范围.
],由正弦函数图象可解得实数m的取值范围.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】某钢厂打算租用![]() ,
,![]() 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材,![]() ,
,![]() 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且![]() 型车皮不多于
型车皮不多于![]() 型车皮7个,分别用
型车皮7个,分别用![]() ,
,![]() 表示租用
表示租用![]() ,
,![]() 两种车皮的个数.
两种车皮的个数.
(1)用![]() ,
,![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(2)分别租用![]() ,
,![]() 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(ax2+4x+5).
(1)若f(1)<3,求a的取值范围;
(2)若a=1,求函数f(x)的值域.
(3)若f(x)的值域为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( ) 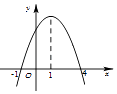
A.在x=﹣1处取得极大值
B.在区间[﹣1,4]上是增函数
C.在x=1处取得极大值
D.在区间[1,+∞)上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
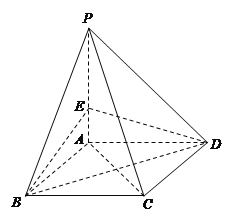
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() 是棱
是棱![]() 上的一个动点.
上的一个动点.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com