
已知在△ABC中,sinA∶sinB∶sinC=3∶5∶7,那么这个三角形的最大角是 ( )
| A.135° | B.90° | C.120° | D.150 |
C
解析试题分析:根据正弦定理化简已知的等式,得到三角形的三边之比,设出三角形的三边,利用余弦定理表示出cosC,把表示出的a,b及c代入即可求出cosC的值,由C的范围,利用特殊角的三角函数值即可求出C的度数,即为三角形最大角的度数.解:设三角形的三边长分别为a,b及c,根据正弦定理 化简已知的等式得: a:b:c=3:5:7,设a=3k,b=5k,c=7k,根据余弦定理得cosC=
化简已知的等式得: a:b:c=3:5:7,设a=3k,b=5k,c=7k,根据余弦定理得cosC=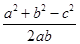 =-
=- ,∵C∈(0,180°),∴C=120°.则这个三角形的最大角为120°.故选D
,∵C∈(0,180°),∴C=120°.则这个三角形的最大角为120°.故选D
考点:正弦定理,以及余弦定理
点评:此题考查了正弦定理,以及余弦定理,遇到比例问题,往往根据比例设出线段的长度来解决问题,熟练掌握定理是解题的关键.


科目:高中数学 来源: 题型:单选题
要测量顶部不能到达的电视塔AB的高度, 在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD="120°," CD="40m," 则电视塔的高度为
A.10 m m | B.20m | C.20 m m | D.40m |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
江岸边有一炮台高30米,江中有两条船,由炮台顶部测得两条船俯角分别为45°和30°,而且两条船与炮台底部连线成30°角,则两条船相距 ( )
| A.150米 | B.120米 | C.100米 | D.30米 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在三棱锥A—BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为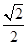 、
、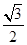 、
、 ,则三棱锥A—BCD的外接球的体积为 ( )
,则三棱锥A—BCD的外接球的体积为 ( )
A.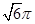 B.2
B.2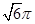 C.3
C.3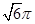 D.4
D.4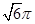
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com