
【题目】已知![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) 函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;(2)
上单调递减;(2) ![]() .
.
【解析】试题分析:
(1)求出导数![]() ,在定义域内,解不等式
,在定义域内,解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(2)题设不等式可变形为
得减区间;(2)题设不等式可变形为![]() ,分别设
,分别设![]() ,
, ![]() ,求出它们的导数
,求出它们的导数![]() ,通过解相应不等式得出单调区间,求出最值,恰好是
,通过解相应不等式得出单调区间,求出最值,恰好是![]() 时,
时, ![]() 取最小值,
取最小值, ![]() 最最大值,因此要使原不等式恒成立,只要
最最大值,因此要使原不等式恒成立,只要![]() 即可.
即可.
试题解析:
(1)由![]() 得:
得: 
由于定义域为![]() ,
,
所以由![]() 得:
得: ![]()
所以由![]() 得:
得: ![]()
即得函数在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减。
上单调递减。
(2)由不等式![]() 恒成立,
恒成立,
即![]() 恒成立
恒成立
设![]() 得:
得:
![]()
因为它们的定义域![]() ,所以易得:
,所以易得:
函数![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增;
上单调递增;
函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减;
上单调递减;
这两个函数在![]() 处,
处, ![]() 有最小值,
有最小值, ![]() 有最大值,
有最大值,
所以要使不等式![]() 恒成立,
恒成立,
则只需满足![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的一段图象如图所示
)的一段图象如图所示 
(1)求f(x)的解析式;
(2)把f(x)的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
(Ⅰ)证明:平面PCE⊥平面PAB;
(Ⅱ)证明:MN∥平面PAC.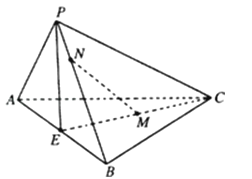
查看答案和解析>>
科目:高中数学 来源: 题型:
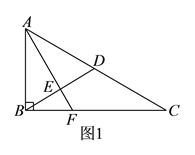
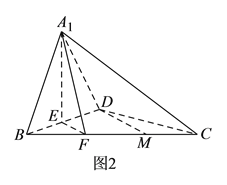
【题目】如图![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() 于
于![]() (不同于点
(不同于点![]() ),延长
),延长![]() 交
交![]() 于
于![]() ,将
,将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,如图
,如图![]() 所示.
所示.
(Ⅰ)若![]() 是
是![]() 的中点,求证:直线
的中点,求证:直线![]() 平面
平面![]() .
.
(Ⅱ)求证: ![]() .
.
(Ⅲ)若平面![]() 平面
平面![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 能否垂直?请说明理由.
能否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:

经过进一步的统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)根据上表给出的数据,用最小二乘法,求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为![]() ,抽到二等奖(价值100元奖品)的概率为
,抽到二等奖(价值100元奖品)的概率为![]() ,抽到三等奖(价值10元奖品)的概率为
,抽到三等奖(价值10元奖品)的概率为![]() ,试估计该分店在此次抽奖活动结束时送出多少元奖品?
,试估计该分店在此次抽奖活动结束时送出多少元奖品?
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为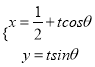 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com