
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
【答案】(1) 详见解析(2) 详见解析(3) 60°.
【解析】
试题分析:(1) 证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要结合平几知识,如三角形中位线性质(2) 证明线面垂直,一般利用线面垂直判定与性质定理,经多次转化给予证明,其中线线垂直的寻找不仅可根据线面垂直关系转化,也可根据平几相关知识进行论证,如等腰三角形底边中线垂直于底边,正方形对角线相互垂直等(3) 先根据二面角定义确定平面角:∠EFD是二面角C-PB-D的平面角.再根据解对应三角形求角.
试题解析:
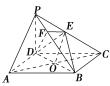
(1)证明 如图所示,
连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,
∴点O是AC的中点.
在△PAC中,EO是中位线,
∴PA∥EO.
而EO平面EDB且PA平面EDB,
∴PA∥平面EDB.
(2)证明 ∵PD⊥底面ABCD,且DC底面ABCD,
∴PD⊥DC.∵PD=DC,可知△PDC是等腰直角三角形.
而DE是斜边PC的中线,∴DE⊥PC.①
同样,由PD⊥底面ABCD,BC平面ABCD,
得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC.又PD∩CD=D,
∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②且PC∩BC=C可推得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,
∴PB⊥平面EFD.
(3)解 由(2)知,PB⊥DF.
故∠EFD是二面角C-PB-D的平面角.
由(2)知DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,
则PD=DC=a,BD=![]() a,
a,
PB=![]() a,PC=
a,PC=![]() a,DE=
a,DE=![]() a,
a,
在Rt△PDB中,DF=![]() a.
a.
在Rt△EFD中,sin∠EFD=![]() ,
,
∴∠EFD=60°.
∴二面角C-PB-D的大小为60°.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
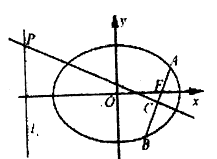
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,直线
,直线![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 和
和![]() 于点
于点![]() .
.
(1)求弦长![]() 的最小值;
的最小值;
(2)在直线![]() 上任取一点
上任取一点![]() ,当
,当![]() 的斜率
的斜率![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
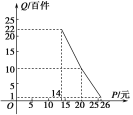
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量![]() =(1,bn),
=(1,bn), ![]() =(an-1,Sn),
=(an-1,Sn), ![]() //
//![]() .
.
(1)若bn=2,求数列{an}通项公式;
(2)若![]() ,
, ![]() =0.
=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足![]() ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得![]() 成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com