
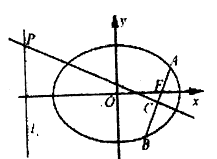
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,直线
,直线![]() ,过右焦点
,过右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 和
和![]() 于点
于点![]() .
.
(1)求弦长![]() 的最小值;
的最小值;
(2)在直线![]() 上任取一点
上任取一点![]() ,当
,当![]() 的斜率
的斜率![]() 时,求
时,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的有__________.(写出所有正确说法的序号)
①已知关于![]() 的不等式
的不等式![]() 的角集为
的角集为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .
.
②已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 、
、![]() 、
、![]() 也构成等比数列.
也构成等比数列.
③已知函数 (其中
(其中![]() 且
且![]() )在
)在![]() 上单调递减,且关于
上单调递减,且关于![]() 的方程
的方程![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则![]() .
.
④已知![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
⑤在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 则
则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
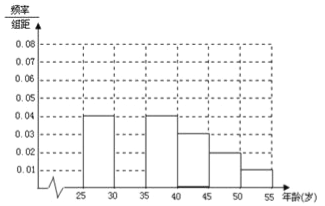
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤ x ≤80时,每天售出的件数为P=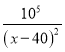 ,每天获得的利润为y(元)
,每天获得的利润为y(元)
(1)写出关于x的函数y的表达式;
(2)若想每天获得的利润最多,问售价应定为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,过
,过![]() 三点的的平面截去长方体的一个角后.得到如图所示的几何体
三点的的平面截去长方体的一个角后.得到如图所示的几何体![]() ,且这个几何体的体积为
,且这个几何体的体积为![]() .
.
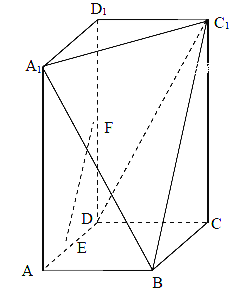
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 的长;
的长;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与
与![]() 垂直,如果存在,求线段
垂直,如果存在,求线段![]() 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC.E是PC的中点,作EF⊥PB交PB于点F.

(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() :
:![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com