
(本小题满分12分)
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.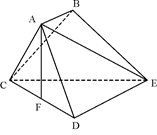
(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求面ACD和面BCE所成锐二面角的大小.
(1)要证明面面垂直 ,则要通过判定定理,先证明DE⊥平面ACD,AF 平面ACD,∴DE⊥AF,以及AF⊥CD,从而得到证明。
平面ACD,∴DE⊥AF,以及AF⊥CD,从而得到证明。
(2) 45°
解析试题分析:解:(Ⅰ)∵DE⊥平面ACD,AF 平面ACD,∴DE⊥AF.
平面ACD,∴DE⊥AF.
又∵AC=AD,F为CD中点,∴AF⊥CD,
因CD∩DE=D,∴AF⊥平面CDE. ……………… 4分
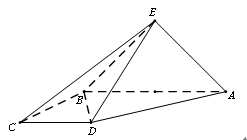
(Ⅱ)取CE的中点Q,连接FQ,因为F为CD的中点,则FQ∥DE,故DE⊥平面ACD,∴FQ⊥平面ACD,又由(Ⅰ)可知FD,FQ,FA两两垂直,以O为坐标原点,建立如图坐标系,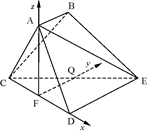
则F(0,0,0),C(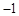 ,0,0),A(0,0,
,0,0),A(0,0,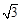 ),B(0,1,
),B(0,1,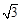 ),E(1,2,0).
),E(1,2,0).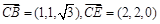
设面BCE的法向量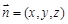 ,则
,则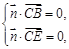
即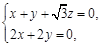 取
取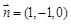 .
.
又平面ACD的一个法向量为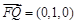 ,
,
∴ 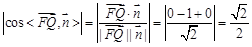 .
.
∴面ACD和面BCE所成锐二面角的大小为45°.
考点:空间中二面角和线面垂直的证明
点评:解决的关键是利用线面垂直的判定定理以及二面角的定义来分析求解,属于基础题 。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,直角梯形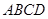 与等腰直角三角形
与等腰直角三角形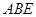 所在的平面互相垂直.
所在的平面互相垂直.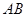 ∥
∥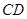 ,
,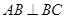 ,
, ,
, .
.
(1)求直线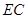 与平面
与平面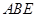 所成角的正弦值;
所成角的正弦值;
(2)线段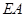 上是否存在点
上是否存在点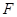 ,使
,使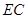 // 平面
// 平面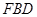 ?若存在,求出
?若存在,求出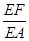 ;若不存在,说明理由.1
;若不存在,说明理由.1
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△BCD中,∠BCD=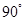 ,BC=CD=1,AB⊥平面BCD,∠ADB=
,BC=CD=1,AB⊥平面BCD,∠ADB=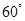 ,E、F分别是AC、AD上的动点,且
,E、F分别是AC、AD上的动点,且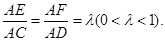
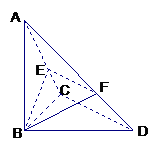
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,已知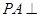 ⊙
⊙ 所在的平面,AB是⊙
所在的平面,AB是⊙ 的直径,
的直径,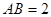 ,
, 是⊙
是⊙ 上一点,且
上一点,且 ,
,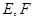 分别为
分别为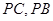 中点。
中点。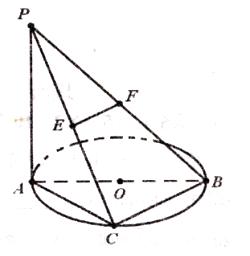
(1)求证: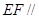 平面
平面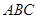 ;
;
(2)求证: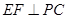 ;
;
(3)求三棱锥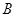 -
-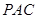 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,三棱锥P-ABC中,PC 平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2, AB=BC,D是PB上一点,且CD 平面PAB
平面PAB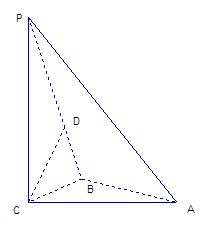
(1)求证:AB 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥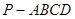 中,底面ABCD是边长为a的正方形,侧面
中,底面ABCD是边长为a的正方形,侧面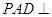 底面ABCD,且
底面ABCD,且 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.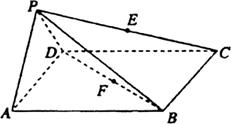
(1)求证: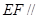 平面PAD;
平面PAD;
(2)求证:平面PDC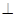 平面PAD;
平面PAD;
(3)求四棱锥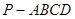 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com