
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是圆内接四边形,
是圆内接四边形,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)设线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且
,且![]() 在线段
在线段![]() 上运动,求直线
上运动,求直线![]() 与平面
与平面![]() 所成角的正弦值的最大值.
所成角的正弦值的最大值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,通过证明
,通过证明![]() 、
、![]() 证得
证得![]() 平面
平面![]() ,由此证得
,由此证得![]() .证得
.证得![]() ,从而证得
,从而证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,设![]() ,通过直线
,通过直线![]() 的方向向量和平面
的方向向量和平面![]() 平面而的法向量求得直线
平面而的法向量求得直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
(1)证明:如图,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
易得![]() ,∴
,∴![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]() .
.
又底面![]() 是圆内接四边形,∴
是圆内接四边形,∴![]() ,
,
在![]() 中,由
中,由![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,易得
,易得![]() ,∴
,∴![]() ,
,
即![]() .又
.又![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
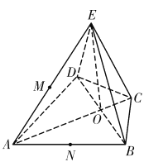
(2)解:点![]() 在线段
在线段![]() 上.以
上.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() ,
,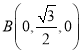 ,
,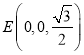 ,
,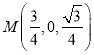 ,
,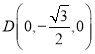 ,
,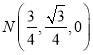 ,∴
,∴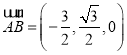 ,
,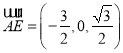 ,
,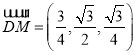 ,
,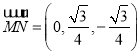 ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则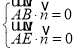 ,即
,即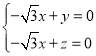 ,令
,令![]() ,则
,则![]() ,
,
设![]() ,可得
,可得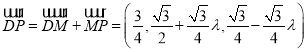 ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则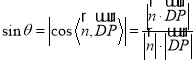
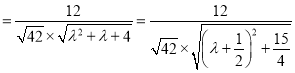 ,
,
∵![]() ,∴当
,∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
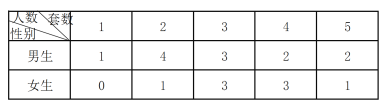
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试判断男学生完成套卷数的方差![]() 与女学生完成套卷数的方差
与女学生完成套卷数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知定点
中,已知定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,设点
,设点![]() 的曲线为
的曲线为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点.
两点.![]()
(1)写出曲线![]() 的方程,并指出曲线
的方程,并指出曲线![]() 的轨迹;
的轨迹;
(2)当![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)证明:存在直线![]() ,满足
,满足![]() ,并求实数
,并求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到点
到点![]() 的距离比它到
的距离比它到![]() 轴的距离多1,记点
轴的距离多1,记点![]() 的轨迹为
的轨迹为![]() ;
;
(1)求轨迹![]() 的方程;
的方程;
(2)求定点![]() 到轨迹
到轨迹![]() 上任意一点
上任意一点![]() 的距离
的距离![]() 的最小值;
的最小值;
(3)设斜率为![]() 的直线
的直线![]() 过定点
过定点![]() ,求直线
,求直线![]() 与轨迹
与轨迹![]() 恰好有一个公共点,两个公共点,三个公共点时
恰好有一个公共点,两个公共点,三个公共点时![]() 的相应取值范围.
的相应取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户考察三种不同的果树苗A、B、C,经引种试验后发现,引种树苗A的自然成活率为0.8,引种树苗B、C的自然成活率均为0.9.
(1)若引种树苗A、B、C各10棵.
①估计自然成活的总棵数;
②利用①的估计结论,从没有自然成活的树苗中随机抽取两棵,求抽到的两棵都是树苗A的概率;
(2)该农户决定引种B种树苗,引种后没有自然成活的树苗中有75%的树苗可经过人工栽培技术处理,处理后成活的概率为0.8,其余的树苗不能成活.若每棵树苗引种最终成活后可获利300元,不成活的每棵亏损50元,该农户为了获利不低于20万元,问至少引种B种树苗多少棵?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com