
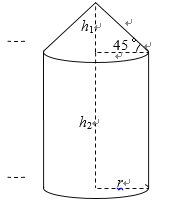
【题目】(题文)如图所示的某种容器的体积为![]() ,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为
,它是由圆锥和圆柱两部分连接而成,圆柱与圆锥的底面半径都为![]() .圆锥的高为
.圆锥的高为![]() ,母线与底面所成的角为
,母线与底面所成的角为![]() ;圆柱的高为
;圆柱的高为![]() ,已知圆柱底面的造价为
,已知圆柱底面的造价为![]() 元
元![]() ,圆柱侧面造价为
,圆柱侧面造价为![]() 元
元![]() ,圆锥侧面造价为
,圆锥侧面造价为![]()
![]() 元
元![]() .
.
(1)将圆柱的高![]() 表示为底面半径
表示为底面半径![]() 的函数,并求出定义域;
的函数,并求出定义域;
(2)当容器造价最低时,圆柱的底面半径![]() 为多少?
为多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】1,4,9,16……这些数可以用图1中的点阵表示,古希腊毕达哥拉斯学派将其称为正方形数,记第![]() 个数为
个数为![]() .在图2的杨辉三角中,第
.在图2的杨辉三角中,第![]() 行是
行是![]() 展开式的二项式系数
展开式的二项式系数![]() ,
,![]() ,…,
,…,![]() ,记杨辉三角的前
,记杨辉三角的前![]() 行所有数之和为
行所有数之和为![]() .
.

(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 |
|
|
|
甲未参加 |
|
|
|
总计 |
|
|
|
(1)求![]() 的值,据此能否有
的值,据此能否有![]() 的把握认为球队胜利与甲球员参赛有关;
的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:![]() ,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:
,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:![]() .则:
.则:
1)当他参加比赛时,求球队某场比赛输球的概率;
2)当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
3)如果你是教练员,应用概率统计有关知识.该如何使用乙球员?
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一年级300名学生对历史、地理学科的选课情况,对学生进行编号,用1,2,…,300表示,并用![]() 表示第
表示第![]() 名学生的选课情况,其中根据如图所示的程序框图,下列说法错误的是( )
名学生的选课情况,其中根据如图所示的程序框图,下列说法错误的是( )

![]()
![]()
A. ![]() 为选择历史的学生人数;
为选择历史的学生人数;
B. ![]() 为选择地理的学生人数;
为选择地理的学生人数;
C. ![]() 为至少选择历史、地理一门学科的学生人数;
为至少选择历史、地理一门学科的学生人数;
D. ![]() 为选择历史的学生人数与选择地理的学生人数之和
为选择历史的学生人数与选择地理的学生人数之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第八章“方程”问题八:今有卖牛二、羊五,以买十三豕,有余钱一千。卖牛三、豕三,以买九羊,钱适足.卖羊六、豕八,以买五牛,钱不足六百.问牛、羊、豕各几何?“如果卖掉2头牛和5只羊,可买13口猪,还余1000钱;卖掉3头牛和3口猪的钱恰好可买9只羊;而卖掉6只羊和8口猪,去买5头牛,还少600钱.问牛、羊、猪的价格各是多少”.按照题意,可解出牛______钱、羊______钱、猪______钱.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励节约用电,辽宁省实行阶梯电价制度,其中每户的用电单价与户年用电量的关系如下表所示.
分档 | 户年用电量(度) | 用电单价(元/度) |
第一阶梯 |
| 0.5 |
第二阶梯 |
| 0.55 |
第三阶梯 |
| 0.80 |
记用户年用电量为![]() 度时应缴纳的电费为
度时应缴纳的电费为![]() 元.
元.
(1)写出![]() 的解析式;
的解析式;
(2)假设居住在沈阳的范伟一家2018年共用电3000度,则范伟一家2018年应缴纳电费多少元?
(3)居住在大连的张莉一家在2018年共缴纳电费1942元,则张莉一家在2018年用了多少度电?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() 的面积为
的面积为![]() ,过点
,过点![]() 的动直线
的动直线![]() 被椭圆
被椭圆![]() 所截得的线段
所截得的线段![]() 长度的最小值为
长度的最小值为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ) ![]() 是椭圆
是椭圆![]() 上异于顶点的一点,且直线
上异于顶点的一点,且直线![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 的半径为
的半径为![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() 的最大值,并求出取得最大值时直线
的最大值,并求出取得最大值时直线![]() 的斜率 .
的斜率 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com