练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校为了解高一年级300名学生对历史、地理学科的选课情况，对学生进行编号，用1,2，…，300表示，并用表示第名学生的选课情况，其中根据如图所示的程序框图，下列说法错误的是( )

    A. 为选择历史的学生人数；

    B. 为选择地理的学生人数；

    C. 为至少选择历史、地理一门学科的学生人数；

    D. 为选择历史的学生人数与选择地理的学生人数之和

    【答案】C

    【解析】分析：读懂程序框图程序框图，得到分别表示的人数含义，从而可得结果.

    详解：阅读程序框图可知，第一个条件语句输出的是择历史的学生人数；

    第二个条件语句输出的是择地理的学生人数；

    为选择历史的学生人数与选择地理的学生人数之和（没有剔除重合部分），

    所以，“为至少选择历史、地理一门学科的学生人数”错误，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第97页B组第3题的函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：

    ①同学甲发现：函数是偶函数；

    ②同学乙发现：对于任意的都有；

    ③同学丙发现：对于任意的，都有；

    ④同学丁发现：对于函数定义域中任意的两个不同实数，总满足.

    其中所有正确研究成果的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四面体中，，则四面体体积最大时，它的外接球半径_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知点是圆心为半径为的半圆弧上从点数起的第一个三等分点，点是圆心为半径为的半圆弧的中点，、分别是两个半圆的直径，，直线与两个半圆所在的平面均垂直，直线、共面.

    （1）求三棱锥的体积；

    （2）求直线与所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，左、右焦点分别为，且，

    ⊙与该椭圆有且只有一个公共点.

    （1）求椭圆标准方程；

    （2）过点的直线与⊙相切，且与椭圆相交于两点，求证：；

    （3）过点的直线与⊙相切，且与椭圆相交于两点，试探究的数量关系.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    某菜园要将一批蔬菜用汽车从所在城市甲运至亚运村乙,已知从城市甲到亚运村乙只有两条公路,且运费由菜园承担.

    若菜园恰能在约定日期(月日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.

    为保证蔬菜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送蔬菜,已知下表内的信息：

    统计信息
    汽车行
    驶路线

    不堵车的情况下到达亚运村乙所需 时间 (天)

    堵车的情况下到达亚运村乙所需时间 (天)

    堵车的
    概率

    运费
    (万元)

    公路1

    2

    3



    公路2

    1

    4



    (注:毛利润销售商支付给菜园的费用运费)

    (Ⅰ) 记汽车走公路1时菜园获得的毛利润为(单位:万元),求的分布列和数学期望；

    (Ⅱ) 假设你是菜园的决策者,你选择哪条公路运送蔬菜有可能让菜园获得的毛利润更多?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）如图所示的某种容器的体积为，它是由圆锥和圆柱两部分连接而成，圆柱与圆锥的底面半径都为．圆锥的高为，母线与底面所成的角为；圆柱的高为，已知圆柱底面的造价为元，圆柱侧面造价为元，圆锥侧面造价为元．

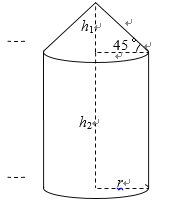
    （1）将圆柱的高表示为底面半径的函数，并求出定义域；

    （2）当容器造价最低时，圆柱的底面半径为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某建材商场国庆期间搞促销活动，规定：顾客购物总金额不超过800元，不享受任何折扣；如果顾客购物总金额超过800元，则超过800元部分享受一定的折扣优惠，并按下表折扣分别累计计算：

    可以享受折扣优惠金额

    折扣率

    不超过500元的部分

    超过500元的部分

    若某顾客在此商场获得的折扣金额为50元，则此人购物实际所付金额为　　

    A.1500元B.1550元C.1750元D.1800元

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“五点法”画函数在某一个周期内的图象时，列表并填入了部分数据，如下表：

    0

    0

    5

    0

    （1）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数的解析式；

    （2）将图象上所有点向左平行移动个单位长度，并把图象上所有点的横坐标缩短为原来的（纵坐标不变），得到的图象.若图象的一个对称中心为，求的最小值；

    （3）在（2）条件下，求在上的增区间.

    查看答案和解析>>

    同步练习册答案