[题目]某学校为了加强学生数学核心素养的培养.锻炼学生自主探究学习的能力.他们以教材第97页B组第3题的函数为基本素材.研究该函数的相关性质.取得部分研究成果如下:①同学甲发现:函数是偶函数,②同学乙发现:对于任意的都有,③同学丙发现:对于任意的.都有,④同学丁发现:对于函数定义域中任意的两个不同实数.总满足.其中所有正确研究成果题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第97页B组第3题的函数为基本素材，研究该函数的相关性质，取得部分研究成果如下：

①同学甲发现：函数是偶函数；

②同学乙发现：对于任意的都有；

③同学丙发现：对于任意的，都有；

④同学丁发现：对于函数定义域中任意的两个不同实数，总满足.

其中所有正确研究成果的序号是__________．

【答案】②③.

【解析】

①利用奇偶函数的定义判断；
②只需要计算等式两端验证即可；
③只需要计算等式两端验证即可；
④根据复合函数单调性判断单调性即可．

解：①定义域关于原点对称，，是奇函数，①错误；
②，②正确；
③由于，

且，则③正确；
④，由于单调递减，单调递增，所以单调递减，，④错误；
故答案为②③．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在某超市，随机调查了100名顾客购物时使用手机支付的情况，得到如下的列联表，已知其中从使用手机支付的人群中随机抽取1人，抽到青年的概率为.

（1）根据已知条件完成列联表，并根据此资料判断是否有的把握认为“超市购物用手机支付与年龄有关”？

（2）现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本，设事件为“从这个样本中任选3人，这3人中至少有2人是使用手机支付的”，求事件发生的概率？

列联表

	青年	中老年	合计
使用手机支付			60
不使用手机支付		28
合计			100

					0.001
					10.828

附：

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数

（1）若关于的不等式的解集为，求实数的值；

（2）设，若不等式对任意实数都成立，求实数的取值范围；

（3）设，解关于的不等式组

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在一个棱长为的正方体的表面涂上颜色，将其适当分割成棱长为的小正方体，全部放入不透明的口袋中，搅拌均匀后，从中任取一个，取出的小正方体表面仅有一个面涂有颜色的概率是（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在圆内接四边形中，，，.

（1）求的大小；

（2）求面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校在本校任选了一个班级，对全班50名学生进行了作业量的调查，根据调查结果统计后，得到如下的列联表，已知在这50人中随机抽取2人，这2人都“认为作业量大”的概率为.

	认为作业量大	认为作业量不大	合计
男生	18
女生		17
合计			50

（1）请完成上面的列联表；

（2）根据列联表的数据，能否有的把握认为“认为作业量大”与“性别”有关？

附表：

	0.100	0.050	0.025	0.010	0.001
	2.706	3.841	5.024	6.635	10.828

附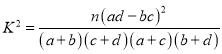：（其中）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】1，4，9，16……这些数可以用图1中的点阵表示，古希腊毕达哥拉斯学派将其称为正方形数，记第个数为.在图2的杨辉三角中，第行是展开式的二项式系数，，…，，记杨辉三角的前行所有数之和为.

（1）求和的通项公式；

（2）当时，比较与的大小，并加以证明.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知如下四个命题：①在线性回归模型中，相关指数表示解释变量对于预报变量的贡献率，越接近于，表示回归效果越好；②在回归直线方程中，当解释变量每增加一个单位时，预报变量平均增加个单位；③两个变量相关性越强，则相关系数的绝对值就越接近于；④对分类变量与，对它们的随机变量的观测值来说，越小，则“与有关系”的把握程度越大．其中正确命题的序号是__________．