练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知α是三角形的内角，且sinα＋cosα＝.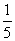

    (1) 求tanα的值；

    (2) 将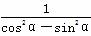用tanα表示出来，并求其值．


    解：(1) (解法1)联立方程

    由①得cosα＝－sinα，

    将其代入②，整理，得25sin2α－5sinα－12＝0.

    ∵ α是三角形内角，∴

    ∴ tanα＝－.

    (解法2)∵ sinα＋cosα＝，∴ (sinα＋cosα)2＝，即1＋2sinαcosα＝，∴ 2sinαcosα＝－，∴ (sinα－cosα)2＝1－2sinαcosα＝1＋＝.

    ∵ sinαcosα＝－<0且0<α<π，∴ sinα>0，cosα<0.

    ∵ sinα－cosα>0，∴ sinα－cosα＝.

    ＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     计算：＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设θ为第二象限角，若tan＝，则sinθ＋cosθ＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝cos(2x＋φ)(－π≤φ≤π)的图象向右平移个单位后，与函数y＝sin的图象重合，则φ＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    α是第二象限角，tanα＝－，则sinα＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知cos(π＋α)＝－，且角α在第四象限，计算：

    (1) sin(2π－α)；

    (2)  (n∈Z)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知在△ABC中，sinA＋cosA＝.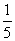

    (1) 求sinA·cosA；

    (2) 判断△ABC是锐角三角形还是钝角三角形；

    (3) 求tanA的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合M＝，N＝{α|－π＜α＜π}，则M∩N＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在平面直角坐标系xOy中，抛物线C的顶点在原点，焦点F的坐标为(1，0)．

    (1) 求抛物线C的标准方程；

    (2) 设M、N是抛物线C的准线上的两个动点，且它们的纵坐标之积为－4，直线MO、NO与抛物线的交点分别为点A、B，求证：动直线AB恒过一个定点．

    查看答案和解析>>

    同步练习册答案