
| A. | 第14项 | B. | 第12项 | C. | 第10项 | D. | 第8项 |
分析 当n为奇数时,可推出an+1=2(an-2+1),从而可得an=${2}^{\frac{n+1}{2}}$-1,从而先解254的前一项,即254=2(${2}^{\frac{n+1}{2}}$-1),从而解得.
解答 解:当n为奇数时,
an=an-1+1=2an-2+1,
故an+1=2(an-2+1),
故an+1=(1+1)•${2}^{\frac{n-1}{2}}$=${2}^{\frac{n+1}{2}}$,
故an=${2}^{\frac{n+1}{2}}$-1,
故254不是奇数项,
故254=2(${2}^{\frac{n+1}{2}}$-1),
故n=13,
故254是该数列的第14项,
故选:A.
点评 本题考查了数列的递推关系的应用及构造法的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
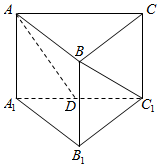 已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )
已知在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
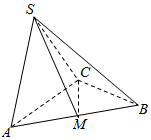 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC=SA=SC,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com