
 如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,
如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,分析 (1)由AB为圆的直径,利用圆周角定理得到∠APB为直角,再由AB=1,表示出PA与PB,根据PT与圆相切,表示出BC,进而表示出四边形ABTP的面积,整理后,利用正弦函数的值域及二次函数性质确定出最大值即可;
(2)把表示出的PA,PB,PC代入所求式子,设t=cosα+sinα,可得出t2=1+2cosαsinα,进而表示出cosαsinα,代入所求式子整理为一个角的正弦函数,利用正弦函数的值域及二次函数性质确定出范围即可.
解答 解:(1)∵AB为直径,
∴∠APB=90°,AB=1,
∵∠PAB=α,
∴PA=cosα,PB=sinα,
又PT切圆于P点,∠TPB=∠PAB=α,
∴BC=sinα•PB=sin2α,
∴S四边形ABTP=S△PAB+S△TPB
=$\frac{1}{2}$PA•PB+$\frac{1}{2}$PT•BC
=$\frac{1}{2}$sinαcosα+$\frac{1}{2}$sin2α
=$\frac{1}{4}$sin2α+$\frac{1}{4}$(1-cos2α)
=$\frac{1}{4}$(sin2α-cos2α)+$\frac{1}{4}$
=$\frac{\sqrt{2}}{4}$sin(2α-$\frac{π}{4}$)+$\frac{1}{4}$,
∵0<α<$\frac{π}{2}$,-$\frac{π}{4}$<2α-$\frac{π}{4}$<$\frac{3}{4}$π,
∴当2α-$\frac{π}{4}$=$\frac{π}{2}$,即α=$\frac{3}{8}$π时,S四边形ABTP最大;
(2)|PA|+|PB|+|PC|=cosα+sinα+sinαcosα,
设t=cosα+sinα,则t2=cos2α+sin2α+2cosαsinα=1+2cosαsinα,
∴cosαsinα=$\frac{{t}^{2}-1}{2}$,
∴|PA|+|PB|+|PC|=$\frac{{t}^{2}-1}{2}$+t=$\frac{{t}^{2}}{2}$+t-$\frac{1}{2}$,
∵t=cosα+sinα=$\sqrt{2}$sin(α+$\frac{π}{4}$)∈(1,$\sqrt{2}$],且t=-1∉(1,$\sqrt{2}$],
∴|PA|+|PB|+|PC|=$\frac{{t}^{2}}{2}$+t-$\frac{1}{2}$在t∈(1,$\sqrt{2}$]时单调递增,
则(|PA|+|PB|+|PC|)∈(1,$\frac{1}{2}$+$\sqrt{2}$].
点评 此题考查了与圆有关的比例线段,正弦函数的定义域与值域,两角和与差的正弦函数公式,以及二次函数性质,熟练掌握三角函数的恒等变换是解本题的关键.


科目:高中数学 来源: 题型:选择题
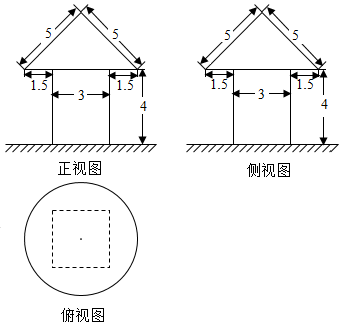 如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )
如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )| A. | 48+24π | B. | 39+24π | C. | 39+36π | D. | 48+30π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2f(x)≥0 | B. | x2f(x)≤0 | C. | x2[f(x)-1]≥0 | D. | x2[f(x)-1]≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com