
分析 由题意知x+f(x)为偶数,奇数加奇数为偶数,偶数加偶数为偶数;说明X中的偶数只能映射为偶数,X中的奇数只能映射为奇数;再确定X分三步,依次定三个元素的对应元素,因此是乘法原理求出.
解答 解:由题意知所谓映射就是集合的对应方法,则就是要看X中的元素对应Y的元素的可行的方法数.
因x+f(x)为偶数且M={-1,0,1},且有奇数加奇数为偶数,偶数加偶数为偶数,
则有下面的情况:
①x=-1,f(x)=-1,1;故有2两种对应方法; ②x=0,f(x)=-2,0,2;故有3两种对应方法;
③x=1,f(x)=-1,1;故有2种对应方法;
∴满足条件的映射有2×3×2=12个.
故答案为:12.
点评 本题考查了映射的定义即是集合的对应方法,利用奇数加奇数为偶数,偶数加偶数为偶数,找出集合M中元素的所有的对应方法,利用分步乘法计数原理求总数.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
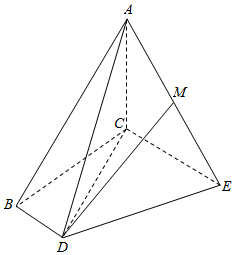 如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.
如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{e}$) | B. | ($\frac{1}{e}$,+∞) | C. | (e,+∞) | D. | (-∞,$\frac{1}{e}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,
如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{π}$ | C. | -$\frac{1}{π}$ | D. | -$\frac{1}{{π}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com