Question

15．我市某大型企业2009年至2015年销售额y（单位：亿元）的数据如表所示：

年份	2009	2010	2011	2012	2013	2014	2015
代号t	1	2	3	4	5	6	7
销售额y	27	31	35	41	49	56	62

（1）画出年份代号与销售额的散点图；

（2）求y关于t的线性回归方程，相关数据保留两位小数；
（3）利用所求回归方程，说出2009年至2015年该大型企业销售额的变化情况，并预测该企业2016年的销售额，相关数据保留两位小数．
附：回归直线的斜率的最小二乘法估计公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t）^{2}}}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$．

Answer 1

分析 （1）有给定的坐标系中描出各组数据对应的点，可得年份代号与销售额的散点图；
（2）根据所给的数据，利用最小二乘法可得代号t和销售额y的平均数，代入公式求出b的值，再求出a的值，写出线性回归方程．
（3）根据（2）求得的线性回归方程，代入所给的t的值，预测该地区2016年的销售额．

解答 解：（1）散点图如图所示，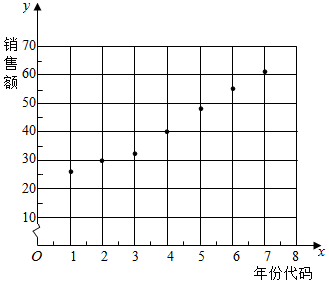


（2）由图表可知：$\overline{t}$=$\frac{1+2+3+4+5+6+7}{7}$=4，
$\overline{y}$=$\frac{27+31+35+41+49+56+62}{7}$=43，
$\sum_{i=1}^{7}$（t_i-$\overline{t}$）²=28，$\sum_{i=1}^{7}$（t_i-$\overline{t}$）（y_i-$\overline{y}$）=169，
$\widehat{b}$=$\frac{\sum_{i=1}^{7}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{7}（{t}_{i}-\overline{t}）^{2}}$≈6.04，
$\stackrel{^}{a}$=$\overline{y}$-$\widehat{b}$•$\overline{t}$=18.84，
∴回归直线方程为y=6.04t+18.84；
（3）2009年至2015年，该企业销售额逐年增长，平均每年增长6.04亿元，2016年时，代号t=8，
y=6.04×8+18.84=67.16，
∴2016年，预测销售额为67.16亿元．

点评 本题考查线性回归分析的应用，利用最小二乘法认真做出线性回归方程的系数是解题的关键，这是整个题目做对的必备条件，属于基础题．