
分析 (1)由已知条件先求出直线l的参数方程,再求出直线l的普通方程,由此能求出直线的极坐标方程.
(2)把圆C的参数方程化为普通方程,把直线参数方程代入x2+y2=4,得${t}^{2}+(\sqrt{3}+1)t-2=0$,由此能示出点P到A,B 两点的距离之和.
解答 解:(1)∵直线l经过点P(1,1),倾斜角α=$\frac{π}{6}$,
∴直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcos\frac{π}{6}}\\{y=1+tsin\frac{π}{6}}\end{array}\right.$,即$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$,…(2分)
直线l的普通方程为:$\sqrt{3}x-3y+3-\sqrt{3}=0$,
所以极坐标方程为$2ρcos(θ+\frac{π}{3})+\sqrt{3}-1=0$…(5分)
(2)圆C的参数方程$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数)化为普通方程为x2+y2=4,
把直线$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}\right.$代入 x2+y2=4,得(1+$\frac{\sqrt{3}}{2}$t)2+(1+$\frac{1}{2}t$)2=4,
∴${t}^{2}+(\sqrt{3}+1)t-2=0$,
t1+t2=$-(\sqrt{3}+1)$,t1×t2=-2,
则点P到A,B 两点的距离之和$|{{t_1}-{t_2}}|=\sqrt{{{({t_1}+{t_2})}^2}-4{t_1}{t_2}}=\sqrt{12+2\sqrt{3}}$.…(10分)
点评 本题考查直线的极坐标方程与参数方程的求法,考查点到两点的距离之和的求法,是中档题,解题时要认真审题,注意极坐标、直角坐标的互化公式的合理运用.


科目:高中数学 来源: 题型:填空题
 如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作与平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A,P两点间的球面距离为$Rarccos\frac{{\sqrt{2}}}{4}$.
如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作与平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A,P两点间的球面距离为$Rarccos\frac{{\sqrt{2}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;
已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
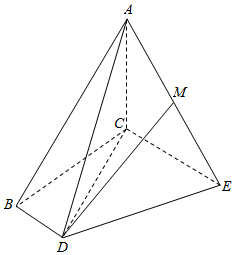 如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.
如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{π}$ | C. | -$\frac{1}{π}$ | D. | -$\frac{1}{{π}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com