
分析 (Ⅰ)设出M点的坐标,由题目条件即可得出动点M的轨迹C的方程;
(Ⅱ)讨论直线l的斜率是否存在,由韦达定理,根据题目条件进行计算即可.
解答 解析:(Ⅰ)设M(x,y),则$|DM|=\sqrt{{{({x+4})}^2}+{y^2}}$,$|EM|=\sqrt{{{({x+1})}^2}+{y^2}}$,
依题意,$\frac{{\sqrt{{{({x+4})}^2}+{y^2}}}}{{\sqrt{{{({x+1})}^2}+{y^2}}}}=2$,
化简整理,得x2+y2=4,
∴曲线c的方程为x2+y2=4.
(Ⅱ)假设直线l存在,设A(x1,y1),B(x2,y2),M(x0,y0)
(1)若直线l的斜率存在,设直线l的方程为:y-1=k(x+1).
联立$\left\{\begin{array}{l}y=k({x+1})+1\\{x^2}+{y^2}-4=0\end{array}\right.$消去y得,(1+k2)x2+2k(k+1)x+k2+2k-3=0,
由韦达定理得,${x_1}+{x_2}=-\frac{{2k({k+1})}}{{1+{k^2}}}$=$-2+\frac{2-2k}{{1+{k^2}}}$,${x_1}{x_2}=\frac{{{k^2}+2k-3}}{{1+{k^2}}}$=$1+\frac{2k-4}{{1+{k^2}}}$,${y_1}{y_2}={k^2}{x_1}{x_2}+k(k+1)({{x_1}+{x_2}})+{(k+1)^2}$=$\frac{2k+4}{{1+{k^2}}}-3$.
∵点A(x1,y1),B(x2,y2)在圆c上,
∴$x_1^2+y_1^2=4$,$x_2^2+y_2^2=4$.
由$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}+\frac{{\sqrt{3}}}{2}\overrightarrow{OB}$得,${x_0}=\frac{{{x_1}+\sqrt{3}{x_2}}}{2}$,${y_0}=\frac{{{y_1}+\sqrt{3}{y_2}}}{2}$.
由于点M也在圆c上,则${(\frac{{{x_1}+\sqrt{3}{x_2}}}{2})^2}+{(\frac{{{y_1}+\sqrt{3}{y_2}}}{2})^2}=4$,
整理得,$\frac{x_1^2+y_1^2}{4}$$+3\frac{x_2^2+y_2^2}{4}$+$\frac{{\sqrt{3}}}{2}{x_1}{x_2}+\frac{1}{2}\sqrt{3}{y_1}{y_2}=4$,
即x1x2+y1y2=0,所以$1+\frac{2k-4}{{1+{k^2}}}$+$(\frac{2k+4}{{1+{k^2}}}-3)=0$,
从而得,k2-2k+1=0,即k=1,因此,直线l的方程为y-1=x+1,即x-y+2=0;
(2)若直线l的斜率不存在,则A(-1,$\sqrt{3}$),B(-1,$-\sqrt{3}$),$M(\frac{{-1-\sqrt{3}}}{2},\frac{{\sqrt{3}-3}}{2})$${(\frac{{-1-\sqrt{3}}}{2})^2}+{(\frac{{\sqrt{3}-3}}{2})^2}=4-\sqrt{3}≠4$,故此时点M不在曲线c上,
综上所知:k=1,直线方程为x-y+2=0.
点评 本题考查轨迹方程的求解,考查学生的计算能力,运用分类讨论的数学思想是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
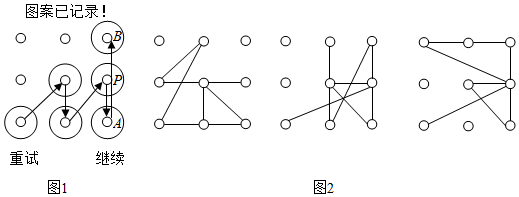
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
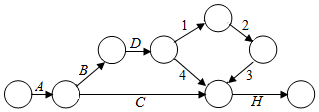 如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.
如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.| 工序代号 | 工序名称或内容 | 紧后工序 |
| A | 拆卸 | B,C |
| B | 清洗 | D |
| C | 电器检修与安装 | H |
| D | 检查零件 | E,G |
| E | 部件维修或更换 | F |
| F | 部件配合试验 | G |
| G | 部件组装 | H |
| H | 装配与试车 |
| A. | E,F,G,G | B. | E,G,F,G | C. | G,E,F,F | D. | G,F,E,F |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AC=4,BD=2,且侧棱AA1=3.其中O1为A1C1与B1D1的交点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AC=4,BD=2,且侧棱AA1=3.其中O1为A1C1与B1D1的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(1)}{4}$<f(2) | B. | $\frac{f(1)}{4}$>f(2) | C. | $\frac{f(2)}{2}$<f(4) | D. | $\frac{f(2)}{2}$>f(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com