
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
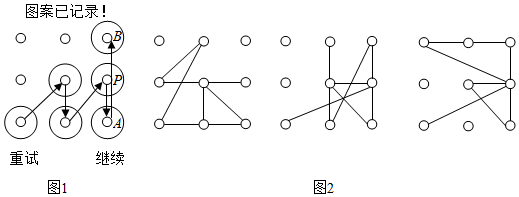
���� ������Ļ����ͼ������ƹ��ɵó����ۣ�
��� �⣺������Ļ����ͼ������ƹ��ӾŸ�����ѡ��һ����Ϊ��㣬��ָ���λ���ijЩ�㣨��ĸ�����1��9��֮�䣩���γ���һ����·ͼ�����ϵĵ�ֻ���״α�����ʱ����ȷ����·�����ã����ڶ��λ��ĵ㲻���Ϊȷ�����ߵĵ㣬
���ֻ֪��һ�ַ������Խ�����Ļ��
���ݢ٣��ڣ��۵���Ϣ���ɵâ٣���ֻ��һ��ʹ��Ψһȷ�������ж��֣�
��ѡ��C��
���� ���⿼��ѧ�����к�������������������ѧ���������͵Ľ�������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������S-ABC�У���ABC�DZ߳�Ϊ4���������Σ�ƽ��SAC��ƽ��ABC��SA=SC=2$\sqrt{3}$��MΪAB���е㣮
������S-ABC�У���ABC�DZ߳�Ϊ4���������Σ�ƽ��SAC��ƽ��ABC��SA=SC=2$\sqrt{3}$��MΪAB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
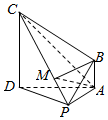 ������P-ABCD�У�CD��ƽ��PAD��AB��CD��AD��PA����ADC����PAD��Ϊ���������Σ�AD=4AB=4��MΪ�߶�CP��һ�㣬��$\overrightarrow{PM}$=��$\overrightarrow{PC}$��0�ܦˡ�1����
������P-ABCD�У�CD��ƽ��PAD��AB��CD��AD��PA����ADC����PAD��Ϊ���������Σ�AD=4AB=4��MΪ�߶�CP��һ�㣬��$\overrightarrow{PM}$=��$\overrightarrow{PC}$��0�ܦˡ�1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���뾶ΪR�İ���O�ĵ���ԲO��ƽ����ڣ�����O��ƽ����Ĵ��߽��������ڵ�A����ԲO��ֱ��CD����ƽ�����45��ǵ�ƽ����������ཻ�����ý����ϵ�ƽ����ľ������ĵ�ΪB���ý����ϵ�һ��P�����BOP=60�㣬��A��P�������������Ϊ$Rarccos\frac{{\sqrt{2}}}{4}$��
��ͼ���뾶ΪR�İ���O�ĵ���ԲO��ƽ����ڣ�����O��ƽ����Ĵ��߽��������ڵ�A����ԲO��ֱ��CD����ƽ�����45��ǵ�ƽ����������ཻ�����ý����ϵ�ƽ����ľ������ĵ�ΪB���ý����ϵ�һ��P�����BOP=60�㣬��A��P�������������Ϊ$Rarccos\frac{{\sqrt{2}}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 2 | B�� | 3 | C�� | $\frac{16}{3}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com