
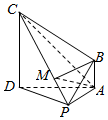
 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).分析 (1)根据线面平行的判定定理即可证明;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可.
解答  解:(1)在PD上取一点E,使PE=$\frac{1}{4}$PD,
解:(1)在PD上取一点E,使PE=$\frac{1}{4}$PD,
∵$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).且λ=$\frac{1}{4}$,
∴ME∥CD,且ME=$\frac{1}{4}$CD,
∵AB∥CD,且AB=$\frac{1}{4}$CD,
∴ME∥AB,ME=AB,
则四边形ABME是平行四边形,
∴MB∥AE,
∵AE?平面PAD,MB?平面PAD,
∴MB∥平面PAD.
(2)建立空间坐标系如图:
则A(0,0,0),C(4,0,4),B(0,0,1),M($\frac{1}{2}$,$\frac{7}{2}$,$\frac{1}{2}$),
$\overrightarrow{AB}$=(0,0,1),$\overrightarrow{AM}$=($\frac{1}{2}$,$\frac{7}{2}$,$\frac{1}{2}$),
设平面ABM的一个法向量为$\overrightarrow{n}$=(x,y,z),
则由$\left\{\begin{array}{l}{\overrightarrow{n•}\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AM}=0}\end{array}\right.$得$\left\{\begin{array}{l}{z=0}\\{\frac{1}{2}x+\frac{7}{2}y+\frac{1}{2}z=0}\end{array}\right.$,令y=1,则$\overrightarrow{n}$=(-7,1,0),
∵AP⊥平面ABC,
∴平面ABC的法向量为$\overrightarrow{m}$=(0,1,0),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{1×1}{1×\sqrt{{7}^{2}+{1}^{2}}}$=$\frac{2}{\sqrt{50}}$=$\frac{\sqrt{2}}{10}$,
∴二面角C-AB-M的余弦值是$\frac{\sqrt{2}}{10}$.
点评 本题主要考查线面平行的判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
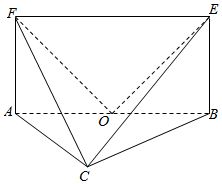 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
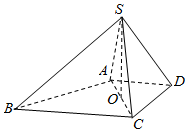 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
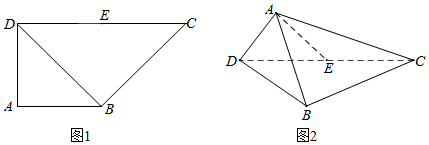
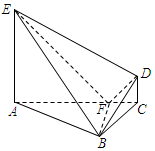 如图,在四棱锥B-ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.
如图,在四棱锥B-ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
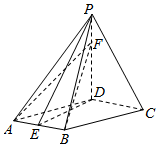 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
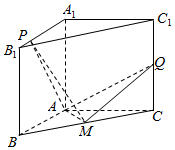 如图,在三棱柱ABC-A1B1C1中,已知AA1=AB=AC,BC=$\sqrt{2}$AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点.
如图,在三棱柱ABC-A1B1C1中,已知AA1=AB=AC,BC=$\sqrt{2}$AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
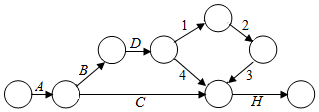 如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.
如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.| 工序代号 | 工序名称或内容 | 紧后工序 |
| A | 拆卸 | B,C |
| B | 清洗 | D |
| C | 电器检修与安装 | H |
| D | 检查零件 | E,G |
| E | 部件维修或更换 | F |
| F | 部件配合试验 | G |
| G | 部件组装 | H |
| H | 装配与试车 |
| A. | E,F,G,G | B. | E,G,F,G | C. | G,E,F,F | D. | G,F,E,F |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com