
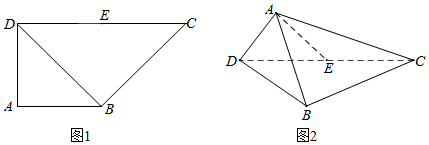
分析 (Ⅰ)在梯形ABCD中,连接BE,推导出四边形ABDE为正方形,AE⊥BD,AF⊥BD,EF⊥BD,从而BD⊥面AEF,由此能证明BD⊥AE.
(Ⅱ)推导出BD⊥BC,EF⊥BD,AF⊥BD,从而∠AFE为二面角A-BD-C的平面角,由此能求出二面角A-BD-C的大小.
解答 证明:(Ⅰ)在梯形ABCD中,连接BE,
因为AB⊥AD,AB=AD=2,所以$BD=2\sqrt{2}$
又$DE=\frac{1}{2}DC=2,AB∥CD$,所以四边形ABDE为正方形,
在梯形ABCD中,连接AE交BD于F,则AE⊥BD…(2分)
翻折过程中,始终有AF⊥BD,EF⊥BD,
又AF∩EF=F,所以BD⊥面AEF,又AE?面AEF,所以BD⊥AE…(5分)
解:(Ⅱ)翻折前,四边形ABDE为正方形,即有BE=2,BE⊥CD,
所以$BC=\sqrt{B{E^2}+E{C^2}}=2\sqrt{2}$,
在△BCD中,$B{D^2}+B{C^2}={({2\sqrt{2}})^2}+{({2\sqrt{2}})^2}=16=C{D^2}$,
所以BD⊥BC…(6分)
因为EF∥BC,所以EF⊥BD,翻折之后,仍有EF⊥BD,
又AF⊥BD,所以∠AFE为二面角A-BD-C的平面角,…(8分)
因为$AD=2,DC=4,AC=2\sqrt{3}$,
所以AD2+AC2=DC2,即AD⊥AC,
因为E为DC的中点,所以$AE=\frac{1}{2}CD=2$.…(10分)
在△AFE中,$AF=\sqrt{A{B^2}-B{F^2}}=\sqrt{2}$,$EF=\frac{1}{2}BC=\sqrt{2}$,AE=2
所以AE2=EF2+AF2,即有EF⊥AF…(11分)
所以二面角A-BD-C为90°.…(12分)
点评 本题考查异面直线垂直的证明,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M为AB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AD=2,AB=1,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2,AB=1,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
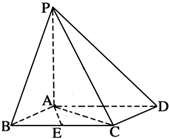 如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
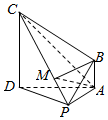 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com