
分析 (1)分类讨论,利用圆心到直线的距离等于半径,建立方程,求出k,即可求过点(4,6)的圆C1的切线方程;
(2)设出过P点的直线l1与l2的点斜式方程,根据⊙C1和⊙C2的半径,及直线l1被圆C1截得的弦长是直线l2被圆C2截得的弦长的2,可得⊙C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离2倍,故我们可以得到一个关于直线斜率k的方程,即可以求所有满足条件的点P的坐标.
解答 解:(1)若切线的斜率存在,可设切线的方程为y-6=k(x-4),
则圆心C1到切线的距离$d=\frac{{|{4k-6}|}}{{\sqrt{1+{k^2}}}}=4$,解得$k=\frac{5}{12}$,
所以切线的方程为:5x-12y+52=0;
若切线的斜率不存在,则切线方程为x=4,符合题意.
综上所述,过P点的圆C1的切线方程为5x-12y+52=0或x=4. …(4分)
(2)设点P(a,b)满足条件,不妨设直线l1的方程为:y-b=k(x-a)(k≠0),
即kx-y+b-ak=0(k≠0),
则直线l2的方程为:$y-b=-\frac{1}{k}(x-a)$,即x+ky-bk-a=0.
因为圆C1的半径是圆C2的半径的2倍,
及直线l1被圆C1截得的弦长是直线l2被圆C2截得的弦长的2倍,
所以圆C1的圆心到直线l1的距离是圆C2的圆心到直线l2的距离的2倍,
即$\frac{{|{b-ak}|}}{{\sqrt{1+{k^2}}}}=2•\frac{{|{7+4k-bk-a}|}}{{\sqrt{1+{k^2}}}}$…(8分)
整理得|ak-b|=|2a-14+(2b-8)k|
从而ak-b=2a-14+(2b-8)k或b-ak=2a-14+(2b-8)k,
即(a-2b+8)k=2a+b-14或(a+2b-8)k=-2a+b+14,
因为k的取值有无穷多个,所以$\left\{\begin{array}{l}a-2b+8=0\\ 2a+b-14=0\end{array}\right.$或$\left\{\begin{array}{l}a+2b-8=0\\-2a+b+14=0\end{array}\right.$,…(11分)
解得$\left\{\begin{array}{l}a=4\\ b=6\end{array}\right.$或$\left\{\begin{array}{l}a=\frac{36}{5}\\ b=\frac{2}{5}\end{array}\right.$,这样点P只可能是点P1(4,6)或点${P_2}(\frac{36}{5},\frac{2}{5})$.
经检验点P1和点P2满足题目条件.…(13分)
点评 本题考查圆的切线方程,考查点到直线的距离公式,直线与圆的位置关系,对称的知识,注意方程无数解的条件,考查转化思想,函数与方程的思想,常考题型,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0,1} | C. | {-1,1} | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
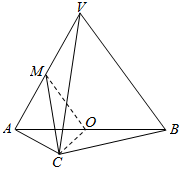 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
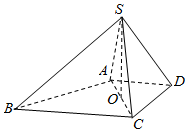 如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.
如图,在底面为梯形的四棱锥S-ABCD中,已知AD∥BC,∠ASC=60°,∠BAD=135°,AD=DC=$\sqrt{2}$,SA=SC=SD=2,O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
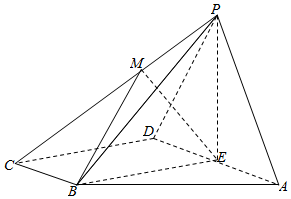
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
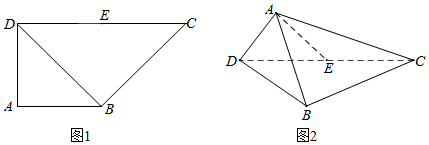
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
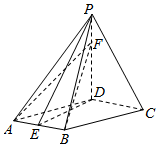 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com