
分析 (Ⅰ)求出函数f(x)的导函数,然后分类讨论,当a≤0时,f(x)的单调增区间为(0,+∞),当a>0时,f(x)的单调增区间为(0,$\frac{2}{a}$),单调递减区间为($\frac{2}{a}$,+∞);
(Ⅱ)求出g(x)的导函数g′(x)=-ax+lnx+a-1 (x>0),当$a<ln\frac{2}{e}$时,g′(x)在(0,+∞)上单调递增,故而g′(x)在(1,2)存在唯一的零点x0,即g′(x0)=0,则当0<x<x0时,g(x)单调递减,当x>x0时,g(x)单调递增,从而可证得结论.
解答 (Ⅰ)解:由函数f(x)=lnx-$\frac{1}{2}$ax+a-2,a∈R.
得$f′(x)=\frac{1}{x}-\frac{a}{2}=\frac{2-ax}{2x}$,(x>0).
若a≤0时,f′(x)>0,函数f(x)的单调递增区间为(0,+∞);
若a>0,$0<x<\frac{2}{a}$时,f′(x)>0,函数f(x)单调递增,
若$x>\frac{2}{a}$时,f′(x)<0,函数f(x)单调递减,
综上,若a≤0时,函数f(x)的单调递增区间为(0,+∞),
若a>0时,函数f(x)的单调递增区间为(0,$\frac{2}{a}$),单调递减区间为($\frac{2}{a}$,+∞);
(Ⅱ)证明:g(x)=xf(x)+2=$xlnx-\frac{1}{2}a{x}^{2}+(a-2)x+2$,(x>0).
则g′(x)=-ax+lnx+a-1 (x>0).
当$a<ln\frac{2}{e}$时,g′(x)=-ax+lnx+a-1在(0,+∞)上单调递增,
又g′(1)=-1<0,$a<ln\frac{2}{e}$,
∴g′(2)=-a+ln2-1>0,
故而g′(x)在(1,2)存在唯一的零点x0,即g′(x0)=0.
则当0<x<x0时,g′(x)<0,g(x)单调递减;
当x>x0时,g′(x)>0,g(x)单调递增;
故而$g(x)≥g({x}_{0})={x}_{0}ln{x}_{0}-\frac{1}{2}a{{x}_{0}}^{2}+$(a-2)x0+2.
又g′(x0)=-ax0+lnx0+a-1=0,1<x0<2,
∴$g(x)≥g({x}_{0})=\frac{1}{2}a{{x}_{0}}^{2}-{x}_{0}+2>2a$.
点评 本题考查了利用导数研究函数的单调性,考查了利用导数研究函数的极值问题,考查了学生的运算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △ABC的重心 | B. | △ABC的内心 | C. | △ABC的外心 | D. | △ABC的垂心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
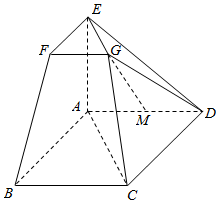 在如图所示的几何体中,四边形ABCD为平行四边形,∠ABC=45°,AB=AC=AE=2EF,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABC=45°,AB=AC=AE=2EF,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M为AB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com