
分析 (1)利用代入法,求动点T的轨迹方程;
(2)设M(-4,m),则圆K方程为x(x+4)+y(y-m)=0与圆O:x2+y2=8联立消去x2,y2得PQ的方程为4x-my+8=0,能够证明直线PQ必过定点E,并求出点E的坐标;
(3)设G(x1,y1),H(x2,y2),则$\left\{\begin{array}{l}{{{x}_{1}}^{2}+2{{y}_{1}}^{2}=8}\\{{{x}_{2}}^{2}+2{{y}_{2}}^{2}=8}\end{array}\right.$,①,知(x1+2,y1)=3(-2-x2,-y2),结合向量求出PQ的方程,由此入手能够求出弦PQ的长.
解答 解:(1)设T(x,y),则|DN|=$\sqrt{2}$|TN|,
∵D为圆O:x2+y2=8上的动点,
∴x2+($\sqrt{2}$y)2=8,
∵|DN|≠0,∴y≠0,
∴动点T的轨迹方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1;
(2)设M(-4,m),则圆K方程为x(x+4)+y(y-m)=0
与圆O:x2+y2=8联立消去x2,y2得PQ的方程为4x-my+8=0,
令y=0,可得x=-2,得直线PQ过定点E(-2,0).
(3)设G(x1,y1),H(x2,y2),则$\left\{\begin{array}{l}{{{x}_{1}}^{2}+2{{y}_{1}}^{2}=8}\\{{{x}_{2}}^{2}+2{{y}_{2}}^{2}=8}\end{array}\right.$,①
∵$\overrightarrow{EG}=3\overrightarrow{HE}$,∴(x1+2,y1)=3(-2-x2,-y2),即:x1=-8-3x2,y1=-3y2,
代入①解得:x2=-$\frac{8}{3}$,y2=±$\frac{2}{3}$(舍去正值),∴kPQ=1,所以PQ:x-y+2=0,
从而圆心O(0,0)到直线PQ的距离d=$\sqrt{2}$,
∴PQ=2$\sqrt{8-2}$=2$\sqrt{6}$.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
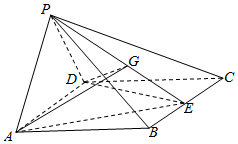 四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E,G分别是BC,PE的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
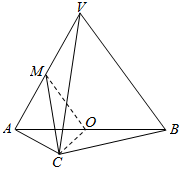 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com