
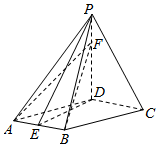
 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.分析 (1)连结BD,推导出△ADB为等边三角形,从而AB⊥DE,由线面垂直得AB⊥PD,由此能证明AB⊥面PED,从而平面PED⊥平面FAB.
(2)由线面垂直得AB⊥PE,连结EF,则AB⊥PE,∠PEF为二面角P-AB-F的平面角,由此能求出二面角P-AB-F的平面角的余弦值.
解答 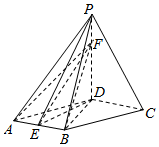 证明:(1)连结BD,
证明:(1)连结BD,
∵AB=AD,∠DAB=60°,∴△ADB为等边三角形,
∵E是AB中点,∴AB⊥DE,
∵PD⊥面ABCD,AB?面ABCD,∴AB⊥PD,
∵DE?面PED,PD?面PED,DE∩PD=D,
∴AB⊥面PED,
∵AB?平面FAB,∴平面PED⊥平面FAB.
解:(2)∵AB⊥平面PED,PE?面PED,∴AB⊥PE,
连结EF,∵EF?面PED,∴AB⊥PE,
∴∠PEF为二面角P-AB-F的平面角,
设AD=4,则PF=1,FD=3,DE=2$\sqrt{3}$,
在△PEF中,PE=2$\sqrt{7}$,EF=$\sqrt{21}$,PF=1,
∴cos∠PEF=$\frac{(2\sqrt{7})^{2}+(\sqrt{21})^{2}-{1}^{2}}{2×2\sqrt{7}×\sqrt{21}}$=$\frac{4\sqrt{3}}{7}$,
∴二面角P-AB-F的平面角的余弦值为$\frac{4\sqrt{3}}{7}$.
点评 本题考查面面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | △ABC的重心 | B. | △ABC的内心 | C. | △ABC的外心 | D. | △ABC的垂心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
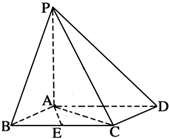 如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
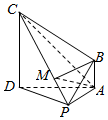 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
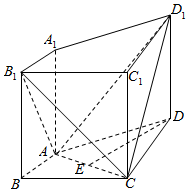 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.用向量法解决下列问题:
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$.用向量法解决下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com