
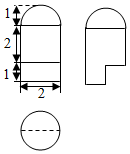
 某几何体的三视图如图所示,则其表面积为( )
某几何体的三视图如图所示,则其表面积为( )| A. | 8π+2 | B. | 10π+2 | C. | 6π+2 | D. | 12π+2 |
科目:高中数学 来源: 题型:解答题
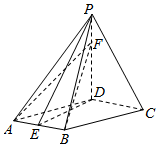 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PA=AD,点E为AB中点,点F在线段PD上,且PF:FD=1:3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{341}{25}$,77] | B. | [$\frac{441}{25}$,81] | C. | [$\sqrt{37}$,77] | D. | [$\frac{1}{5}$,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
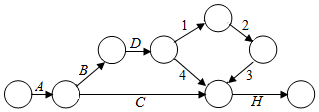 如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.
如表为某设备维修的工序明细表,其中“紧后工序”是指一个工序完成之后必须进行的下一个工序.| 工序代号 | 工序名称或内容 | 紧后工序 |
| A | 拆卸 | B,C |
| B | 清洗 | D |
| C | 电器检修与安装 | H |
| D | 检查零件 | E,G |
| E | 部件维修或更换 | F |
| F | 部件配合试验 | G |
| G | 部件组装 | H |
| H | 装配与试车 |
| A. | E,F,G,G | B. | E,G,F,G | C. | G,E,F,F | D. | G,F,E,F |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
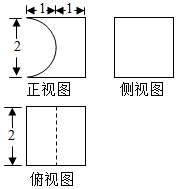 祖暅原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高,意思是两个同高的几何体,如在等高处截面的面积恒相等,体积相等.已知某不规则几何体与如图所示的几何体满足“幂势同”,则该不规则几何体的体积为( )
祖暅原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高,意思是两个同高的几何体,如在等高处截面的面积恒相等,体积相等.已知某不规则几何体与如图所示的几何体满足“幂势同”,则该不规则几何体的体积为( )| A. | 4-$\frac{π}{2}$ | B. | 8-$\frac{4π}{3}$ | C. | 8-π | D. | 8-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AC=4,BD=2,且侧棱AA1=3.其中O1为A1C1与B1D1的交点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AC=4,BD=2,且侧棱AA1=3.其中O1为A1C1与B1D1的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
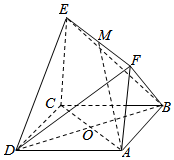 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=$\sqrt{2}$,AF=1,M是线段EF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com