
| A. | [$\frac{341}{25}$,77] | B. | [$\frac{441}{25}$,81] | C. | [$\sqrt{37}$,77] | D. | [$\frac{1}{5}$,5] |
分析 把$\overrightarrow{PE}•\overrightarrow{PF}$转化为($\overrightarrow{NE}$-$\overrightarrow{NP}$)•($\overrightarrow{NF}$-$\overrightarrow{NP}$)=$\overrightarrow{NE}$•$\overrightarrow{NF}$-$\overrightarrow{NP}$•($\overrightarrow{NE}$+$\overrightarrow{NF}$)+$\overrightarrow{NP}$2=-|NE|•|NF|•cosπ-0+|NP|2=-4+|NP|2.
再结合|NP|的范围即可求出结论.
解答 解:$\overrightarrow{PE}•\overrightarrow{PF}$=($\overrightarrow{NE}$-$\overrightarrow{NP}$)•($\overrightarrow{NF}$-$\overrightarrow{NP}$)
=$\overrightarrow{NE}$•$\overrightarrow{NF}$-$\overrightarrow{NP}$•($\overrightarrow{NE}$+$\overrightarrow{NF}$)+$\overrightarrow{NP}$2
=-|NE|•|NF|•cosπ-0+|NP|2
=-4+|NP|2.
点N(1,0)到直线$\frac{x}{8}+\frac{y}{6}$=1的距离为$\frac{|6-48|}{\sqrt{36+64}}$=$\frac{21}{5}$,
∵点P(x,y)是曲线$\frac{|x|}{8}+\frac{|y|}{6}=1$上的动点,
∴|NP|∈[$\frac{21}{5}$,9]
∴$\overrightarrow{PE}•\overrightarrow{PF}$∈[$\frac{341}{25}$,77].
故选:A.
点评 本题主要考查圆的基本性质.解决本题的关键在于会把所求问题转化.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
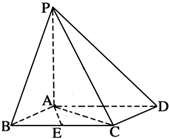 如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,F是PC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
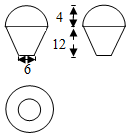
| A. | 81π | B. | 125π | C. | (41+7$\sqrt{145}$)π | D. | (73+7$\sqrt{145}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
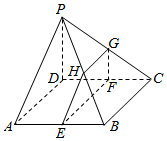 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,AD=PD,∠DAB=60°.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为菱形,AD=PD,∠DAB=60°.点分E,F,G,H别是棱AB,CD,PC,PB上共面的四点,且BC∥EF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com