
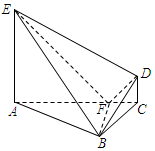
 如图,在四棱锥B-ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.
如图,在四棱锥B-ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.分析 方法一(几何法):(Ⅰ)推导出AE⊥BF,BF⊥AC,从而BF⊥DF,再求出CD⊥平面ABC,从而CD⊥AC,进而DF⊥EF,由此能证明DF⊥平面BEF,从而得到DF⊥BE.
(Ⅱ)过点F作FG⊥DE于点G,连接BG,则∠BGF二面角B-DE-F的平面角,由此能求出二面角B-DE-F的平面角的余弦值.
方法二(向量法):(Ⅰ)过F作Fz∥AE,以F为原点,FA.FB.Fz依次为x.y.z轴建立空间直角坐标系,利用向量法能证明DF⊥BE.
(Ⅱ)求出平面DEF的一个法向量和平面BDE的一个法向量,利用向量法能求出二面角B-DE-F的平面角的余弦值.
解答  (本小题共12分)
(本小题共12分)
方法一(几何法):
证明:(Ⅰ)∵AE⊥平面ABC,BF?平面ABC,∴AE⊥BF,
∵BF⊥AC,AE∩AC=A,
∴BF⊥平面AEC,DF?平面AEC,∴BF⊥DF,…(2分)
∵∠ABC=3∠BAC=90°,又AC=4CD=4,
∴∠BAC=30°.CD=1.
∴$BC=ACsin{30°}=4×\frac{1}{2}=2$,
又BF⊥AC.∴$CF=BCcos{60°}=2×\frac{1}{2}=1=CD$,
又CD∥AE,AE⊥平面ABC,∴CD⊥平面ABC.
又AC?平面ABC.∴CD⊥AC,∴∠DFC=45°.
又AF=AC-CF=3=AE,∴∠EFA=45°,
∴∠EFD=90°,即DF⊥EF.…..…(4分)
又BF∩EF=F,BF.EF?平面BEF.
∴DF⊥平面BEF,BE?平面BEF.
∴DF⊥BE.…(6分)
解:(Ⅱ)如图,过点F作FG⊥DE于点G,连接BG.
由(Ⅰ)知BF⊥平面AEC,又DE?平面AEC,∴BF⊥DE.
又BF∩FG=F,BF.FG?平面BFG,∴DE⊥平面BFG.
又BG?平面BFG,∴BG⊥FG.(三垂线定理)
故∠BGF二面角B-DE-F的平面角.…(8分)
在Rt△EAF中,$EF=\sqrt{E{A^2}+A{F^2}}=\sqrt{{3^2}+{3^2}}=3\sqrt{2}$.
在Rt△FCD中,$FD=\sqrt{F{C^2}+C{D^2}}=\sqrt{{1^2}+{1^2}}=\sqrt{2}$.….…(9分)
在Rt△EFD中,$ED=\sqrt{E{F^2}+F{D^2}}=\sqrt{{{(3\sqrt{2})}^2}+{{(\sqrt{2})}^2}}=2\sqrt{5}$.
由EF•FD=FG•ED得$FG=\frac{EF•FD}{ED}=\frac{{3\sqrt{2}×\sqrt{2}}}{{2\sqrt{5}}}=\frac{{3\sqrt{5}}}{5}$.…(10分)
在Rt△BFC中,$BF=\sqrt{B{C^2}-F{C^2}}=\sqrt{{2^2}-{1^2}}=\sqrt{3}$.
在Rt△BFG中,$BG=\sqrt{B{F^2}+F{G^2}}=\sqrt{3+\frac{9}{5}}=\frac{{2\sqrt{30}}}{5}$.…(11分)
∴$cos∠BFG=\frac{FG}{BG}=\frac{{\frac{{3\sqrt{5}}}{5}}}{{\frac{{2\sqrt{30}}}{5}}}=\frac{{\sqrt{6}}}{4}$.
∴二面角B-DE-F的平面角的余弦值为$\frac{{\sqrt{6}}}{4}$.….(12分)
方法二(向量法):
证明:(Ⅰ)过F作Fz∥AE,由AE⊥平面ABC可知Fz⊥平面ABC,
又AC.BF?平面ABC,于是Fz⊥AC,Fz⊥BF,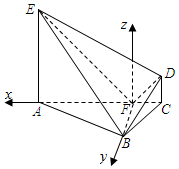
又BF⊥AC,∴BF.AC.Fz两两垂直.
以F为原点,FA.FB.Fz依次为x.y.z轴建立空间直角坐标系(如图).…(1分)
∵∠ABC=3∠BAC=90°,AC=4CD=4,AE=3,
∴CD=1,∠BAC=30°.
∴$BC=\frac{1}{2}AC=2$,$FC=BC•cos{60°}=2×\frac{1}{2}=1$,AF=AC-FC=3,$BF=\sqrt{B{C^2}-F{C^2}}=\sqrt{3}$.…(3分)
于是F(0,0,0),$B(\;0\;,\;\sqrt{3}\;,\;0\;)$,D(-1,0,1),E(3,0,3),$\overrightarrow{FD}=(\;-1\;,\;0\;,\;1\;)$,$\overrightarrow{BE}=(\;3\;,\;-\sqrt{3}\;,\;3\;)$.
故$\overrightarrow{FD}•\overrightarrow{BE}=-1×3+0×(-\sqrt{3})+1×3=0$.
所以DF⊥BE…..…(6分);
解:(Ⅱ)由(Ⅰ)知$\overrightarrow{FE}=(\;3\;,\;0\;,\;3\;)$,$\overrightarrow{BD}=(\;-1\;,\;-\sqrt{3}\;,\;1\;)$,$\overrightarrow{BE}=(\;3\;,\;-\sqrt{3}\;,\;3\;)$,$\overrightarrow{FB}=(\;0\;,\;\sqrt{3}\;,\;0\;)$.
于是$\overrightarrow{FB}•\overrightarrow{FE}=0×3+\sqrt{3}×0+0×3=0$,所以FB⊥FE,又FB⊥AC.
所以$\overrightarrow{FB}$是平面DEF的一个法向量.…..…(8分)
设$\overrightarrow n=(\;x\;,\;y\;,\;z\;)$是平面BDE的一个法向量,则$\left\{\begin{array}{l}\overrightarrow{n\;}•\overrightarrow{BD}=-x-\sqrt{3}y+z=0\\ \overrightarrow{n\;}•\overrightarrow{BE}=3x-\sqrt{3}y+3z=0\end{array}\right.$
取z=2,得到$\overrightarrow n=(\;-1\;,\;\sqrt{3}\;,\;2\;)$.…(10分)
∴$cos<\overrightarrow{n\;\;},\;\overrightarrow{FB}>\;=\frac{{\overrightarrow{n\;}•\overrightarrow{FB}}}{{|\overrightarrow{n\;}|•|\overrightarrow{FB}|}}=\frac{3}{{2\sqrt{2}•\sqrt{3}}}=\frac{{\sqrt{6}}}{4}$.
又二面角B-DE-F是锐二面角.
∴二面角B-DE-F的平面角的余弦值为$\frac{{\sqrt{6}}}{4}$.…(12分)
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
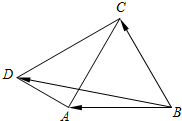 如图,在四边形ABCD中,△ABC是边长为6的正三角形,设$\overrightarrow{BD}=x\overrightarrow{BA}+y\overrightarrow{BC}$(x,y∈R).
如图,在四边形ABCD中,△ABC是边长为6的正三角形,设$\overrightarrow{BD}=x\overrightarrow{BA}+y\overrightarrow{BC}$(x,y∈R).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.
如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在矩形ABCD中,AD=2,AB=1,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2,AB=1,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
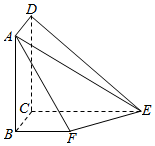 如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
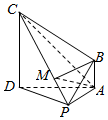 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
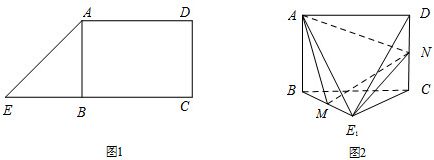
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作与平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A,P两点间的球面距离为$Rarccos\frac{{\sqrt{2}}}{4}$.
如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作与平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A,P两点间的球面距离为$Rarccos\frac{{\sqrt{2}}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com