
 已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;
已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;分析 (1)利用距离公式,即可用x1表示|OA|;
(2)分类讨论,计算|OA|•|OB|,即可证明|OA|•|OB|为定值;
(3)由(2)得|OA|•|OB|=3,同理|OC||OD|=3,利用基本不等式,即可得出结论.
解答 (1)解:设A(x1,y1),代入圆E:(x-1)2+y2=4,得y12=-x12+2x1+3,
∴|OA|=$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$=$\sqrt{2{x}_{1}+3}$;
(2)证明:设B(x2,y2),
同理可得|OB|=$\sqrt{2{x}_{2}+3}$,
∴|OA|•|OB|=$\sqrt{4{x}_{1}{x}_{2}+6({x}_{1}+{x}_{2})+9}$
x1≠x2,设直线AB的方程为y=kx,代入圆的方程得(k+1)x2-2x-3=0,
∴x1+x2=$\frac{2}{{k}^{2}+1}$,x1x2=-$\frac{3}{{k}^{2}+1}$,
代入可得|OA|•|OB|=3,
x1=x2,直线过原点,直线AB的方程为x=0,即x1=x2=0,代入可得|OA|•|OB|=3,
综上所述,|OA|•|OB|=3为定值;
(3)解:由(2)得|OA|•|OB|=3,同理|OC||OD|=3
∴S1+S2=$\frac{1}{2}$(|OA||OC|+|OB||OD|)≥$\sqrt{|OA||OC||OB||OD|}$=3,当且仅当|OA||OC|=|OB||OD|时取等号,
此时,S1+S2最小值为3,直线AB的方程为y=±x.
点评 本题考查直线与圆的位置关系,考查分类讨论的数学思想,考查基本不等式的运用,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
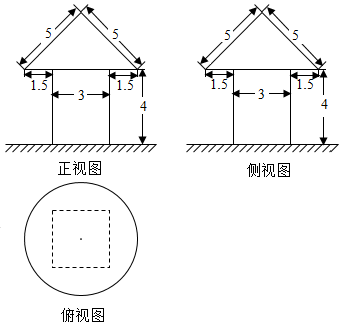 如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )
如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )| A. | 48+24π | B. | 39+24π | C. | 39+36π | D. | 48+30π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin(2πx-$\frac{π}{2}$) | B. | sin($\frac{π}{2}$x-$\frac{π}{2}$) | C. | sin(πx-$\frac{π}{2}$) | D. | sin(πx+$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )
某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )| A. | $\frac{10}{33}$ | B. | $\frac{13}{36}$ | C. | $\frac{13}{23}$ | D. | $\frac{23}{33}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com