
���� ����ֱ��l�IJ���������ȥ����t�ɵã�����ֱ�����귽�̣���ԲC�ļ����귽�����ݻ�����ʽת��Ϊֱ�����귽�̣�
����ֱ��l������ԲC�ķ������������飬���A��B��������꣬�ɵ�|PA|+|PB|��ֵ��
��� �⣺����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$��tΪ����������ȥ����t�ɵ�3x+$\sqrt{3}$y-3=0��
ԲC�ķ���Ϊ��=2$\sqrt{3}$sin�ȣ��� ��2=2$\sqrt{3}$��sin�ȣ��� x2+y2=2$\sqrt{3}$y���� x2+${��y-\sqrt{3}��}^{2}$=3��
������$\left\{\begin{array}{l}{3x+\sqrt{3}y-3=0}\\{{x}^{2}{+��y-\sqrt{3}��}^{2}=3}\end{array}\right.$��� $\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}}\\{y=\sqrt{3}-\frac{3}{2}}\end{array}\right.$����$\left\{\begin{array}{l}{x=-\frac{\sqrt{3}}{2}}\\{y=\sqrt{3}+\frac{3}{2}}\end{array}\right.$��
�ʿɵ�A��$\frac{\sqrt{3}}{2}$��$\sqrt{3}$-$\frac{3}{2}$����B��-$\frac{\sqrt{3}}{2}$��$\sqrt{3}$+$\frac{3}{2}$����
�ߵ�P��1��0������|PA|+|PB|=$\sqrt{{��1-\frac{\sqrt{3}}{2}��}^{2}{+��0-\sqrt{3}+\frac{3}{2}��}^{2}}$+$\sqrt{{��1+\frac{\sqrt{3}}{2}��}^{2}{+��0-\sqrt{3}-\frac{3}{2}��}^{2}}$=��2-$\sqrt{3}$ ��+��2+$\sqrt{3}$��=4��
���� ������Ҫ������������뼫���ꡢֱ������Ļ��������������ߵĽ��㣬���ڻ����⣮


 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
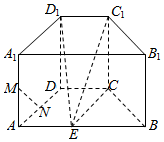 ��ͼ����ֱ������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ�AB��CD��AB=4��BC=CD=2��AA1=2��M��N�ֱ�����AA1��AD���е㣬��E����AB���е㣮
��ͼ����ֱ������ABCD-A1B1C1D1�У�����ABCDΪ�������Σ�AB��CD��AB=4��BC=CD=2��AA1=2��M��N�ֱ�����AA1��AD���е㣬��E����AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
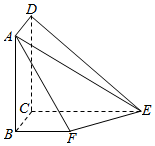 ��ͼ��ʾ��DC��ƽ��BCEF�����ı���ABCDΪ���Σ��ı���BCEFΪֱ�����Σ�BF��CE��BC��CE��DC=CE=4��BC=BF=2��
��ͼ��ʾ��DC��ƽ��BCEF�����ı���ABCDΪ���Σ��ı���BCEFΪֱ�����Σ�BF��CE��BC��CE��DC=CE=4��BC=BF=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4$\sqrt{3}$ | B�� | 5 | C�� | 3$\sqrt{3}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���뾶ΪR�İ���O�ĵ���ԲO��ƽ����ڣ�����O��ƽ����Ĵ��߽��������ڵ�A����ԲO��ֱ��CD����ƽ�����45��ǵ�ƽ����������ཻ�����ý����ϵ�ƽ����ľ������ĵ�ΪB���ý����ϵ�һ��P�����BOP=60�㣬��A��P�������������Ϊ$Rarccos\frac{{\sqrt{2}}}{4}$��
��ͼ���뾶ΪR�İ���O�ĵ���ԲO��ƽ����ڣ�����O��ƽ����Ĵ��߽��������ڵ�A����ԲO��ֱ��CD����ƽ�����45��ǵ�ƽ����������ཻ�����ý����ϵ�ƽ����ľ������ĵ�ΪB���ý����ϵ�һ��P�����BOP=60�㣬��A��P�������������Ϊ$Rarccos\frac{{\sqrt{2}}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪ԲE����x-1��2+y2=4���߶�AB��CD����ԲE���ң���AB��CD��ֱ���ཻ������ԭ��O����ͼ��ʾ�����AOC�����ΪS1�����BOD�����ΪS2��
��֪ԲE����x-1��2+y2=4���߶�AB��CD����ԲE���ң���AB��CD��ֱ���ཻ������ԭ��O����ͼ��ʾ�����AOC�����ΪS1�����BOD�����ΪS2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com