
分析 (1)推导出[f(xi+1)-f(xi)]=f(xi)-f(xi+1),从而S=$\sum_{i=0}^{n-1}$|f(xi+1)-f(xi)|=f(x0)-f(xn)=f(-1)-f(1),由此能求出S的值.
(2)由${f}^{'}(x)=\frac{1-x}{{e}^{x}}$=0,得x=1,由导数性质得f(x)在x=1时,取极大值$\frac{1}{e}$.设xm≤1<xm+1,m∈N,m≤n-1,由此能求出S=$\sum_{i=0}^{n-1}|f({x}_{i+1})-f({x}_{i})|$的最大值.
(3)${f}^{'}(x)=\frac{k}{x}-x=\frac{k-{x}^{2}}{x}$,x∈[1,e],根据当k≥e2,k≤1和1<k<e2三种情况进行分类讨论,利用导数性质能证明对于给定的实数k,函数f(x)=klnk-$\frac{1}{2}{x}^{2}$在[1,e]上具有性质V.
解答 解:(1)∵函数f(x)=-2x+1在区间[-1,1]为减函数,
∴f(xi+1)<f(xi),∴[f(xi+1)-f(xi)]=f(xi)-f(xi+1),
S=$\sum_{i=0}^{n-1}$|f(xi+1)-f(xi)|=[f(x0)-f(x1)]+[f(x1)-f(x2)]+…+[f(xn-1)-f(xn)]
=f(x0)-f(xn)
=f(-1)-f(1)=4.
(2)由${f}^{'}(x)=\frac{1-x}{{e}^{x}}$=0,得x=1,
当x<1时,f′(x)>0,∴f(x)在(-∞,1)为增函数,
当x>1时,f′(x)<0,∴f(x)在(1,+∞)为减函数,
∴f(x)在x=1时,取极大值$\frac{1}{e}$.
设xm≤1<xm+1,m∈N,m≤n-1,
则S=$\sum_{i=0}^{n-1}|f({x}_{i+1})-f({x}_{i})|$
=|f(x1)-f(0)|+…+|f(xm)-f(xm-1)|+|f(xm+1)-f(xm)|+|f(xm+2)-f(xm+1)|+…|f(2)-f(xn-1)|
=[f(x1)-f(0)]+…+[f(xm)-f(xm-1)]+|f(xm+1)-f(xm)|+|f(xm+1)-f(xm+2)|+…+[f(xn-1)-f(2)]
=[f(xm)-f(0)]+|f(xm+1)-f(xm)|+[f(xm+1)-f(2)],
∵|f(xm+1)-f(xm)|≤[f(1)-f(xm)]+[f(1)-f(xm+1)],当xm=1时取等号,
∴S≤f(xm)-f(0)+f(1)-f(xm+1)+f(1)-f(xm+1)+f(xm+1)-f(2)
=2f(1)-f(0)-f(2)=$\frac{2(e-1)}{{e}^{2}}$.
∴S的最大值为$\frac{2(e-1)}{{e}^{2}}$.
证明:(3)${f}^{'}(x)=\frac{k}{x}-x=\frac{k-{x}^{2}}{x}$,x∈[1,e],
①当k≥e2时,k-x2≥0恒成立,即f′(x)≥0恒成立,∴f(x)在[1,e]上为增函数,
∴S=$\sum_{i=0}^{n-1}|f({x}_{i+1})-f({x}_{i})|$=[f(x1)-f(x0)]+[f(x2)-f(x1)]+…+[f(xn)-f(xn-1)]
=f(xn)-f(x0)=f(e)-f(1)=k+$\frac{1}{2}-\frac{1}{2}{e}^{2}$.
∴存在正数A=k+$\frac{1}{2}-\frac{1}{2}{e}^{2}$,都有S≤A,
∴f(x)在[1,e]上具有性质V.
②当k≤1时,k-x2≤0恒成立,即f′(x)≤0恒成立,∴f(x)在[1,e]上为减函数,
∴S=$\sum_{i=0}^{n-1}$|f(xi+1)-f(xi)|=[f(x0)-f(x1)]+[f(x1)-f(x2)]+…+[f(xn-1)-f(xn)]
=f(x0)-f(xn)=f(1)-f(e)=$\frac{1}{2}{e}^{2}-k-\frac{1}{2}$.
∴存在正数A=$\frac{1}{2}{e}^{2}-k-\frac{1}{2}$,都有S≤A,
∴f(x)在[1,e]上具有性质V.
③当1<k<e2时,由f′(x)=0,得x=$\sqrt{k}$,由f′(x)>0,得1$≤x<\sqrt{k}$;
由f′(x)<0,得$\sqrt{k}$<x≤e,∴f(x)在[1,$\sqrt{k}$)上为增函数,在[$\sqrt{k}$,e]上为减函数,
设xm≤$\sqrt{k}$<xm+1,m∈N,m≤n-1,
则S=$\sum_{i=1}^{n-1}$|f(xi+1)-f(xi)|
=|f(xi)-f(x0)|+…+|f(xm)-f(xm-1)|+|f(xm+1)-f(xm)||+|f(xm+2)-f(xm+1)|+…+|f(xn)-f(xn-1)|
=f(x1)-f(x0)+…+f(xm)-f(xm-1)+|f(xm+1)-f(xm)|+f(xm+1)-f(xm+2)+…+f(xn-1)-f(xn)
=f(xm)-f(x0)+f(xm+1)-f(xn)+f($\sqrt{k}$)-f(xm+1)+f($\sqrt{k}$)-f(xm)
=2f($\sqrt{k}$)-f(x0)-f(xn)
=klnk-k-[-$\frac{1}{2}+k-\frac{1}{2}{e}^{2}$]
=klnk-2k+$\frac{1}{2}+\frac{1}{2}{e}^{2}$,
∴存在正数A=klnk-2k+$\frac{1}{2}+\frac{1}{2}{e}^{2}$,都有S≤A,
∴f(x)在[1,e]上具有性质V.
综上,对于给定的实数k,函数f(x)=klnk-$\frac{1}{2}{x}^{2}$在[1,e]上具有性质V.
点评 本题考查函数值的求法,考查函数值的最大值的求法,考查函数具有某种性质的证明,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
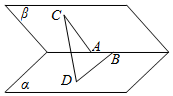 如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长.
如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
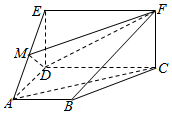 如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.
如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.
如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )
某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )| A. | $\frac{10}{33}$ | B. | $\frac{13}{36}$ | C. | $\frac{13}{23}$ | D. | $\frac{23}{33}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com