
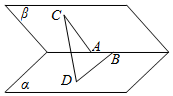
 如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长.
如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长. 分析 根据二面角的大小,利用向量的数量积的应用即可求CD的长度.
解答 解:由已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,$\overrightarrow{BD}$⊥$\overrightarrow{AB}$,即$\overrightarrow{AB}$•$\overrightarrow{BD}$=0,$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,<$\overrightarrow{AC}$,$\overrightarrow{BD}$>=45°,
∵$\overrightarrow{CD}=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${|{\overrightarrow{CD}}|^2}={(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD})^2}={|{\overrightarrow{CA}}|^2}+{|{\overrightarrow{AB}}|^2}+{|{\overrightarrow{BD}}|^2}+2|{\overrightarrow{CA}}||{\overrightarrow{BD}}|cos{135°}$
=$1+3+2-2|{\overrightarrow{AC}}||{\overrightarrow{BD}}|cos{45°}=4$,
∴CD=2
点评 本题主要考查向量数量积的应用,结合二面角的大小运用向量法是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
| 身高x(cm) | 160 | 165 | 170 | 175 | 180 |
| 体重y(kg) | 65 | 69 | m | 72 | 74 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
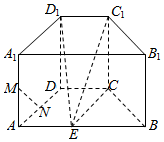 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分别是棱AA1、AD的中点,设E是棱AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分别是棱AA1、AD的中点,设E是棱AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.
如图在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=CC1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
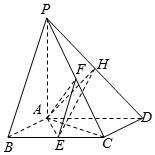 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
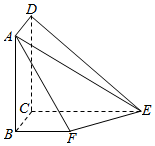 如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com