练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知以下三视图中有三个同时表示某一个三棱锥，则不是该三棱锥的三视图是（　　）
    A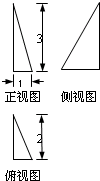．B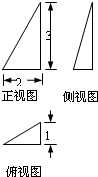．C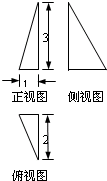．D．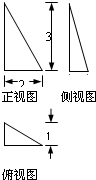

    分析 由已知中的四个三视图，可知四个三视图，分别表示从前、后、左、右四个方向观察同一个棱锥，但其中有一个是错误的，根据A与C中俯视图正好旋转180°，故应是从相反方向进行观察，而其正视图和侧视图中三角形斜边倾斜方向相反，满足实际情况，可得A，C均正确，而根据AC可判断B正确，D错误

    解答 解：三棱锥的三视图均为三角形，四个答案均满足；
    且四个三视图均表示一个高为3，底面为两直角边分别为1，2的棱锥
    A与C中俯视图正好旋转180°，故应是从相反方向进行观察，而其正视图和侧视图中三角形斜边倾斜方向相反，满足实际情况，故A，C表示同一棱锥
    设A中观察的正方向为标准正方向，以C表示从后面观察该棱锥
    B与D中俯视图正好旋转180°，故应是从相反方向进行观察，但侧视图中三角形斜边倾斜方向相同，不满足实际情况，故B，D中有一个不与其它三个一样表示同一个棱锥，
    根据B中正视图与A中侧视图相同，侧视图与C中正视图相同，可判断B是从左边观察该棱锥
    故选D．

    点评 本题考查的知识点是空间几何体的三视图，本题要求具有超强的空间想像能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．已知偶函数f（x）在区间[0，+∞）内单调递减，f（2）=0．若f（x-1）＞0，则x的取值范围是（　　）
    A．（-2，2）B．（-1，2）C．（2，+∞）D．（-1，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．函数f（x）=$\frac{a}{x}$+lnx，其中a为实常数．
    （1）讨论f（x）的单调性；
    （2）不等式f（x）≥1在x∈（0，1]上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知圆锥的底面半径为1，高为$2\sqrt{2}$，则该圆锥的侧面积为3π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．要证明不等式$\sqrt{3}$+$\sqrt{7}$＜2$\sqrt{5}$，可选择的方法有（　　）
    A．分析法B．综合法
    C．反证法D．以上三种方法均可

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若函数f（x）=2x2-4x+1，则f（x）的最小值为（　　）
    A．-3B．-2C．-1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

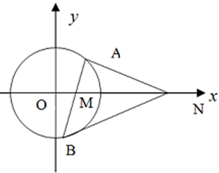    16．已知直线l：4x+3y+10=0，半径为2的圆C与l相切，圆心C在x轴上且在直线l的右上方
    （1）求圆C的方程；
    （2）过点M（1，0）的直线与圆C交于A，B两点（A在x轴上方），问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

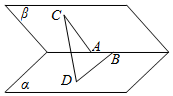    13．如图所示，45°的二面角的棱上有两点A，B，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AC=1，AB=$\sqrt{3}$，BD=$\sqrt{2}$，求CD的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

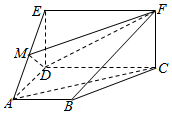    14．如图，在多面体ABCDEF中，CDEF为矩形，ABCD为直角梯形，平行CDEF⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=$\frac{1}{2}$CD=1，ED=$\sqrt{3}$，M为线段EA上动点．
    （Ⅰ）若M为EA中点，求证：AC∥平面MDF；
    （Ⅱ）线段EA上是否存在点M，使平面MDF与平面ABCD所成的锐二面角大小为$\frac{π}{3}$？若存在，求出AM的长度，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案