
| A. | 分析法 | B. | 综合法 | ||
| C. | 反证法 | D. | 以上三种方法均可 |
分析 利用三种方法,给出不等式的证明,即可得出结论.
解答 解:用分析法证明如下:要证明$\sqrt{3}$+$\sqrt{7}$<2$\sqrt{5}$,
需证($\sqrt{3}$+$\sqrt{7}$)2<(2$\sqrt{5}$)2,
即证10+2$\sqrt{21}$<20,
即证$\sqrt{21}$<5,即证21<25,显然成立,
故原结论成立.
综合法:∵($\sqrt{3}$+$\sqrt{7}$)2-(2$\sqrt{5}$)2=10+2 $\sqrt{21}$-20=2($\sqrt{21}$-5)<0,∴$\sqrt{3}$+$\sqrt{7}$<2$\sqrt{5}$.
反证法:假设$\sqrt{3}$+$\sqrt{7}$≥2$\sqrt{5}$通过两端平方后导出矛盾,从而肯定原结论.
从以上证法中,可知三种方法均可.
故选:D.
点评 本题考查分析法、综合法、反证法的应用,考查分析与判定思维能力,属于中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | 1-$\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{\sqrt{2}}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
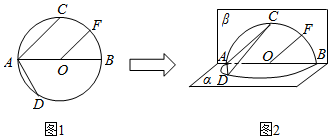
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E
已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com