
分析 (1)由题意可得k≥$\frac{1+lnx}{x}$,令h(x)=$\frac{1+lnx}{x}$,求得导数和单调区间,可得最大值,即可得到k的范围;
(2)由(1)知,lnx≤x-1,当且仅当x=1时,取等号.令x=1+$\frac{1}{{n}^{2}}$(n∈N*,n≥2),有ln(1+$\frac{1}{{n}^{2}}$)<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,运用数列的求和方法:裂项相消求和,结合不等式的性质即可得证.
解答 (1)解:函数f(x)=lnx-kx+1,f(x)≤0有kx≥1+lnx,x>0,
即k≥$\frac{1+lnx}{x}$,令h(x)=$\frac{1+lnx}{x}$,h′(x)=$\frac{-lnx}{{x}^{2}}$=0,解得x=1,
在(0,1)上,h′(x)>0;在(1,+∞)上,h′(x)<0.
所以h(x)在x=1时,取得最大值h(1)=1,即k≥1;
(2)证明:由(1)知,当k=1时,lnx≤x-1,当且仅当x=1时,取等号.
令x=1+$\frac{1}{{n}^{2}}$(n∈N*,n≥2),
有ln(1+$\frac{1}{{n}^{2}}$)<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
所以有ln(1+$\frac{1}{{2}^{2}}$)<1-$\frac{1}{2}$,ln(1+$\frac{1}{{3}^{2}}$)<$\frac{1}{2}$-$\frac{1}{3}$,…,ln(1+$\frac{1}{{n}^{2}}$)<$\frac{1}{n-1}$-$\frac{1}{n}$,
累加得:ln($\frac{5}{4}$)+ln($\frac{10}{9}$)+ln($\frac{17}{16}$)+…+ln($\frac{{{n^2}+1}}{n^2}$)<1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$=1-$\frac{1}{n}$<1(n∈N*,n≥2).
点评 本题考查不等式恒成立问题的解法,注意运用参数分离和构造函数法,考查不等式的证明,注意运用不等式的性质和累加法,考查运算化简能力,属于中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 分析法 | B. | 综合法 | ||
| C. | 反证法 | D. | 以上三种方法均可 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
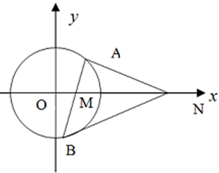 已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
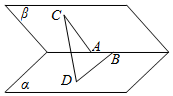 如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长.
如图所示,45°的二面角的棱上有两点A,B,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AC=1,AB=$\sqrt{3}$,BD=$\sqrt{2}$,求CD的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
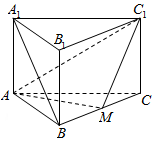 如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
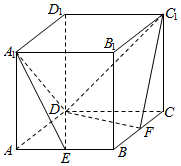 如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB、BC的中点,则平面A1DE与平面C1DF所成二面角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB、BC的中点,则平面A1DE与平面C1DF所成二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com