
 已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E
已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E分析 (Ⅰ)利用代入法,求曲线E的方程;
(Ⅱ)分类讨论,设直线l:y=kx+2与椭圆方程联立,利用韦达定理,向量得出坐标关系,求出直线的斜率,即可求直线l的方程.
解答 解:(I)设M(x,y),则P(x,2y)在圆x2+4y2=4上,如图1,
所以x2+4y2=4,即$\frac{x^2}{4}+{y^2}=1$…..(4分)
(II)经检验,当直线l⊥x轴时,题目条件不成立,所以直线l存在斜率如图2.
设直线l:y=kx+2.设C(x1,y1),D(x2,y2),
则$\left\{\begin{array}{l}\frac{x^2}{4}+{y^2}=1\\ y=kx+2\end{array}\right.⇒(1+4{k^2}){x^2}+16kx+12=0$.…(6分)
△=(16k)2-4(1+4k2)•12>0,得${k^2}>\frac{3}{4}$.
${x_1}+{x_2}=-\frac{16k}{{1+4{k^2}}}$….①,${x_1}{x_2}=\frac{12}{{1+4{k^2}}}$…②.…(8分)
又由$\overrightarrow{AC}=\frac{3}{5}\overrightarrow{AD}$,得${x_1}=\frac{3}{5}{x_2}$,
将它代入①,②得k2=1,k=±1(满足${k^2}>\frac{3}{4}$).
所以直线l的斜率为k=±1.所以直线l的方程为y=±x+2…(12分)
点评 本题考查代入法求轨迹方程,考查直线与椭圆的位置关系,考查韦达定理、向量知识的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 分析法 | B. | 综合法 | ||
| C. | 反证法 | D. | 以上三种方法均可 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
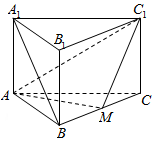 如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.
如图,已知三棱柱A1B1C1-ABC中,侧棱与底面垂直,AB=BC=AA1,∠ABC=90°,M是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
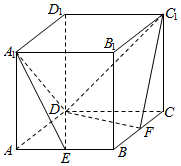 如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB、BC的中点,则平面A1DE与平面C1DF所成二面角的余弦值为( )
如图,在正方体ABCD-A1B1C1D1中,E,F分别是棱AB、BC的中点,则平面A1DE与平面C1DF所成二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
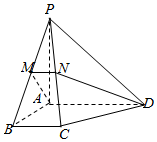 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过AD的平面分别交PB,PC于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
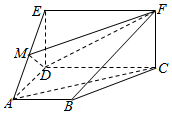 如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.
如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com