
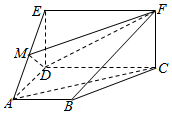
 如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.
如图,在多面体ABCDEF中,CDEF为矩形,ABCD为直角梯形,平行CDEF⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1,ED=$\sqrt{3}$,M为线段EA上动点.分析 (Ⅰ)连结CE交DF于O,则OM∥AC,由此能证明AC∥平面MDF.
(Ⅱ)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出当AM=(2$\sqrt{3}$-3)AE时,平面MDF与平面ABCD所成锐二面角的大小为$\frac{π}{3}$.
解答  证明:(Ⅰ)连结CE交DF于O,
证明:(Ⅰ)连结CE交DF于O,
∵CDEF为矩形,∴O为CE中点,
又M为EA中点,∴OM∥AC,
又AC?平面MDF,OM?平面MDF,
∴AC∥平面MDF.
解:(Ⅱ)假设线段EA上存在点M,使平面MDF与平面ABCD所成的锐二面角大小为$\frac{π}{3}$.
理由如下:
∵平面CDEF⊥平面ABCD,
在矩形CDEF中,ED⊥DC,平面CDEF∩平面ABCD=CD,
∴ED⊥平面ABCD,AD?平面ABCD,∴ED⊥AD,
又CD⊥AD,∴以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
则D(0,0,0),A(1,0,0),E(0,0,$\sqrt{3}$),F(0,2,$\sqrt{3}$),
由题意知M,E重合时不符合,设$\overrightarrow{AM}=λ\overrightarrow{AE}$,(0≤λ<1),
则M(1-λ,0,$\sqrt{3}λ$),$\overrightarrow{DM}$=(1-λ,0,$\sqrt{3}λ$),$\overrightarrow{DF}$=(0,2,$\sqrt{3}$),
设$\overrightarrow{n}$=(x,y,z)是平面DMF的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DM}=(1-λ)x+\sqrt{3}λz=0}\\{\overrightarrow{n}•\overrightarrow{DF}=2y+\sqrt{3}z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=($\frac{\sqrt{3}λ}{λ-1}$,-$\frac{\sqrt{3}}{2}$,1),
又ED⊥平面ABCD,∴平面ABCD的法向量$\overrightarrow{m}$=(0,0,1),
∵线段EA上存在点M,使平面MDF与平面ABCD所成的锐二面角大小为$\frac{π}{3}$,
∴cos$\frac{π}{3}$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{(\frac{\sqrt{3}λ}{λ-1})^{2}+(-\frac{\sqrt{3}}{2})^{2}+1}}$=$\frac{1}{2}$,
解得$λ=2\sqrt{3}-3$∈[0,1],或$λ=-(2\sqrt{3}+3)∉$[0,1],(舍去),
∴当AM=(2$\sqrt{3}$-3)AE时,平面MDF与平面ABCD所成锐二面角的大小为$\frac{π}{3}$,
此时AM=4$\sqrt{3}-6$.
点评 本题考查线面平行的证明,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
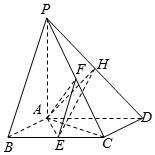 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,且AC=BC=2,PA⊥平面ABCD,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
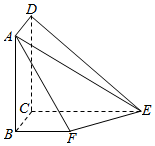 如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E
已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足$\overrightarrow{PM}$=$\overrightarrow{MP}$,当P在圆C上运动时,点M形成的轨迹为曲线E查看答案和解析>>
科目:高中数学 来源: 题型:解答题
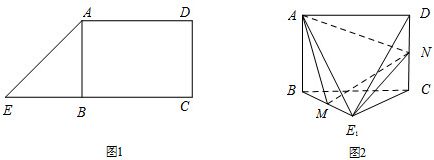
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 5 | C. | 3$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
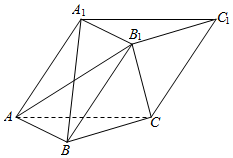 如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.
如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com