
分析 (1)曲线C的极坐标方程为ρ=4cosθ,得ρ2=4ρcosθ,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出.由直线l过点M(3,0),倾斜角为$\frac{π}{6}$,可得参数方程.
(2)把直线l代入圆的直角坐标方程x2+y2-4x=0,得${({3+\frac{{\sqrt{3}}}{2}t})^2}+\frac{1}{4}{t^2}-4({3+\frac{{\sqrt{3}}}{2}t})=0$,化简后利用韦达定理可求t1+t2,t1t2的值,由|MA|+|MB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$即可求值得解.
解答 (本题满分10分)
解:(1)对于C:由ρ=4cosθ,得ρ2=4ρcosθ,
∵$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,
∴x2+y2=4x,
∴对于l:有$\left\{{\begin{array}{l}{x=3+\frac{{\sqrt{3}}}{2}t}\\{y=\frac{1}{2}t}\end{array}({t为参数})}\right.$.
(2)设A,B两点对应的参数分别为t1,t2
将直线l的参数方程带入圆的直角坐标方程x2+y2-4x=0,
得${({3+\frac{{\sqrt{3}}}{2}t})^2}+\frac{1}{4}{t^2}-4({3+\frac{{\sqrt{3}}}{2}t})=0$,
化简得${t^2}+\sqrt{3}t-3=0$,
$\begin{array}{l}∴{t_1}+{t_2}=-\sqrt{3},{t_1}{t_2}=-3\\∴|{MA}|+|{MB}|=|{t_1}|+|{t_2}|=|{{t_1}-{t_2}}|=\sqrt{{{({{t_1}+{t_2}})}^2}-4{t_1}{t_2}}=\sqrt{15}\end{array}$
点评 本题考查了极坐标方程化为直角坐标方程、直线参数方程、弦长公式,考查了计算能力,属于中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
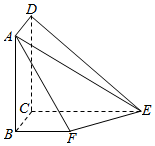 如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.
如图所示,DC⊥平面BCEF,且四边形ABCD为矩形,四边形BCEF为直角梯形,BF∥CE,BC⊥CE,DC=CE=4,BC=BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
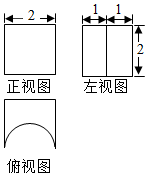 某几何体的三视图如图所示,其中俯视图下半部分是半径为1的半圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图下半部分是半径为1的半圆,则该几何体的表面积是( )| A. | 20+2π | B. | 20+π | C. | 20-2π | D. | 20-π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
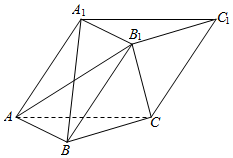 如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.
如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;
已知圆E:(x-1)2+y2=4,线段AB、CD都是圆E的弦,且AB与CD垂直且相交于坐标原点O,如图所示,设△AOC的面积为S1,设△BOD的面积为S2;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{e}$) | B. | ($\frac{1}{e}$,+∞) | C. | (e,+∞) | D. | (-∞,$\frac{1}{e}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com