
分析 先根据两个截面圆的面积分别求出对应圆的半径,再分析出两个截面所存在的两种情况,最后对每一种情况分别求出两个平行平面的距离即可.
解答 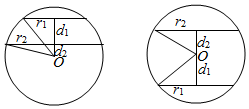 解:设球心到截面的距离分别为d1,d2,球的半径为R.
解:设球心到截面的距离分别为d1,d2,球的半径为R.
如图①所示.当球的球心在两个平行平面的外侧时,
这两个平面间的距离为球心与两个截面圆的距离之差.
即d2-d1=$\sqrt{1{0}^{2}-{6}^{2}}$-$\sqrt{1{0}^{2}-{8}^{2}}$=8-6=2.
如图②所示.当球的球心在两个平行平面的之间时,
这两个平面间的距离为球心与两个截面圆的距离之和.
即d2+d1=$\sqrt{1{0}^{2}-{6}^{2}}$+$\sqrt{1{0}^{2}-{8}^{2}}$=8+6=14.
故答案为:2或14.
点评 本题主要考查两个平行平面间的距离计算问题.此题重点考查球中截面圆半径,球半径之间的关系以及空间想象能力和计算能力.本题的易错点在于只考虑一种情况,从而漏解.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.
如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
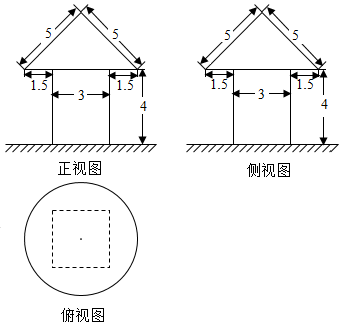 如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )
如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )| A. | 48+24π | B. | 39+24π | C. | 39+36π | D. | 48+30π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com