
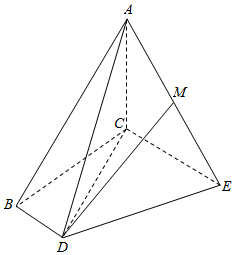
 如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.
如图所示,△ABC是边长为2的正三角形,EC⊥平面ABC,DB⊥平面ABC,且M为AE的中点,CE=CA=2BD.分析 (1)利用线面垂直的判定定理即可证明DM∥平面ABC;
(2)根据面面垂直的判定定理即可证明平面DEA⊥平面ECA;
(3)利用体积法建立方程即可求点E到平面ACD的距离
解答 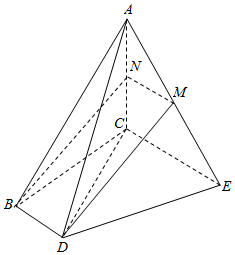 证明:(1)过点M在△ABC中作MN∥CE,交AC于N,连接BN,
证明:(1)过点M在△ABC中作MN∥CE,交AC于N,连接BN,
∵CE⊥平面AB,DB⊥平面ABC
∴CE∥DB
又∵CE=2BD=2,M为AE的中点
∴NM∥CE,NM=$\frac{1}{2}$CE
∴NM∥BD,NM=BD,
∴四边形DMNB是平行四边形
∴DM∥BN
又∵BN平面?ABC,DM?平面ABC
∴DM∥平面ABC….(4分)
(2)∵CE⊥平面ABC BN?平面ABC∴CE⊥BN 即BN⊥CE
又∵△ABC是边长为2的等边三角形且N为AC中点∴BN⊥AC
又∵AC∩CE=C AC,CE?平面ACE∴BN⊥平面ACE
由第(1)问知:BN∥DM
∴DM⊥平面ACE 又∵DM?平面DEA
∴平面DEA⊥平面AEC ….(8分)
(3)∵CE⊥平面ABC,AC?平面AB∴CE⊥AC
又∵CE=AC=2,∴${S}_{△ACE}=\frac{1}{2}×2×2=2$
由第(1)、(2)问知:DM⊥平面ABC;DM=BN=$\sqrt{3}$
又∵DB⊥平面ABC,AB?平面ABC∴DB⊥AB
即在Rt△DBC中,CD=$\sqrt{4+1}$=$\sqrt{5}$
∴在△ADC中,AD=CD=$\sqrt{5}$,AC=2
∴${S}_{△ACD}=\frac{1}{2}×2×\sqrt{5-1}=2$ …(10分)
设点E到平面ACD的距离为h,
则 $\frac{1}{3}•{S}_{ACE}•DM=\frac{1}{3}•{S}_{△ACD}•h$,即 2-$\sqrt{3}$=2-h,∴h=$\sqrt{3}$
即点E到平面ACD的距离为$\sqrt{3}$ …..(12分)
点评 本题主要考查空间直线和平面平行以及面面垂直的判断以及点到平面的距离的计算,利用体积法是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.
如图,E是矩形ABCD中AD边上的点,F是CD上的点,AB=AE=$\frac{2}{3}$AD=4,现将△ABE沿BE边折至△PBE位置,并使平面PBE⊥平面BCDE,且平面PBE⊥平面PEF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
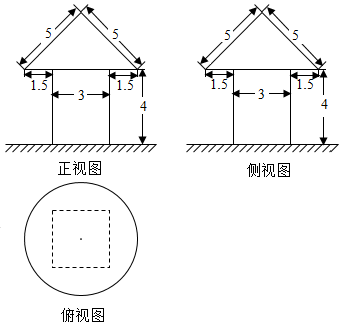 如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )
如图是一建筑物的三视图(单位:米),现需将其外壁用油漆刷一遍,若每平方米用漆1千克,则共需油漆的总量(单位:千克)为( )| A. | 48+24π | B. | 39+24π | C. | 39+36π | D. | 48+30π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )
某三棱柱被一个平面截去一部分后所得的几何体的三视图如图所示,其中俯视图是边长为2的正三角形,则截去部分和剩余部分的体积之比为( )| A. | $\frac{10}{33}$ | B. | $\frac{13}{36}$ | C. | $\frac{13}{23}$ | D. | $\frac{23}{33}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{f(1)}{4}$<f(2) | B. | $\frac{f(1)}{4}$>f(2) | C. | $\frac{f(2)}{2}$<f(4) | D. | $\frac{f(2)}{2}$>f(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com