考点:数列的求和,排列、组合的实际应用
专题:计算题,压轴题,等差数列与等比数列,二项式定理
分析:(1)由二项式定理得递推公式:a
n+1=a
n+
,b
n+1=b
n+
,从而求a
n=1-
()n,b
n=
-
+
;
(2)假设存在,则
(1+
)(1+
)=
-
+
,化简得p+q=-3,pq=2,从而解出p=-2,q=-1.
解答:
解:(1)∵f(x,n)=(1+
)(1+
)…(1+
)=g(x,n)x
3+b
nx
2+a
nx+1,
∴f(x,n+1)=f(x,n)(1+
),
∴g(x,n+1)x
3+b
n+1x
2+a
n+1x+1=[g(x,n)x
3+b
nx
2+a
nx+1](1+
)
比较x系数有:a
n+1=a
n+
,比较x
2系数有:b
n+1=b
n+
,
又∵a
1=
,b
1=0;
∴a
n=
+
()2+…+
()n=1-
()n;
∴b
n+1=b
n+
=b
n+
-
;
∴b
n=b
1+(
+
+…+
)-(
+
+…+
)
=0+(
-
)-
(1-
)
=
-
+
;
∴a
n=1-
()n,b
n=
-
+
;
(2)若存在常数p.q(p<q),使b
n=
(1+
)(1+
),对n∈N
*,n≥2恒成立,
则有
(1+
)(1+
)=
-
+
,
即(1+
)(1+
)=1-3
+2
()2,
则p+q=-3,pq=2,
解得p=-2,q=-1.
点评:本题考查了二项式的分解及由递推公式求通项公式的方法,同时考查了拆项求和与公式法求和,属于压轴题.化简也比较困难,需要细心.



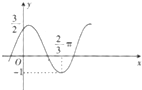 将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移
将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移