
【题目】抛掷两枚质地均匀的硬币,设事件A=“第一枚硬币正面朝上”,事件B=“第二枚硬币反面朝上”.
(1)写出样本空间,并列举A和B包含的样本点;
(2)下列结论中正确的是( ).
A.A与B互为对立事件 B.A与B互斥 C.A与B相等 D.P(A)=P(B)
【答案】(1)解:样本空间可表示为Ω={(正,正),(正,反),(反,正),(反,反)}.A包含的样本点:(正,正),(正,反).B包含的样本点:(正,反),(反,反).
(2)D
【解析】
(1)列举出抛掷两枚质地均匀的硬币所有可能的情况,即可得出样本空间以及A和B包含的样本点;
(2)利用互斥事件与对立事件的定义判断![]() 选项,由相等事件的定义判断
选项,由相等事件的定义判断![]() ;计算出事件
;计算出事件![]() 的概率即可得出正确答案.
的概率即可得出正确答案.
(1) 抛掷两枚质地均匀的硬币,所有可能的情况为:(正,正),(正,反),(反,正),(反,反)
则样本空间为Ω={(正,正),(正,反),(反,正),(反,反)}
A包含的样本点:(正,正),(正,反)
B包含的样本点:(正,反),(反,反)
(2)由于事件![]() 能同时发生,则事件
能同时发生,则事件![]() 既不互斥也不对立;
既不互斥也不对立;
事件![]() 中有不同的样本点,则事件
中有不同的样本点,则事件![]() 不相等;
不相等;
![]() ,
,![]() ,则
,则![]()
故选:D


科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
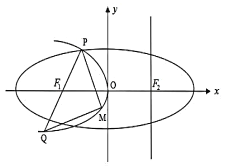
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列的定义可用数学符号语言描述为_______,其中![]() ,其通项公式
,其通项公式![]() _________,
_________,![]() ______,等比数列中,若
______,等比数列中,若![]() 则_________(
则_________(![]() ),若
),若![]() ,则
,则![]() 的等比中项为____.
的等比中项为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中,随机抽取100名,按年龄(单位:岁)进行统计的频率分布直方图如图:

(1)根据频率分布直方图,分别求出样本的平均数(同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位);
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加华为手机宣传活动,再从这20人中年龄在![]() 和
和![]() 的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在
的人群里,随机选取2人各赠送一部华为手机,求这2名市民年龄都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】使用支付宝和微信支付已经成为广大消费者最主要的消费支付方式,某超市通过统计发现一周内超市每天的净利润![]() (万元)与每天使用支付宝和微信支付的人数
(万元)与每天使用支付宝和微信支付的人数![]() (千人)具有相关关系,并得到最近一周
(千人)具有相关关系,并得到最近一周![]() 的7组数据如下表,并依此作为决策依据.
的7组数据如下表,并依此作为决策依据.
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
13 | 16 | 26 | 22 | 25 | 29 | 30 |
7 | 11 | 15 | 22 | 24 | 27 | 34 |
(Ⅰ)作出散点图,判断![]() 与
与![]() 哪一个适合作为每天净利润的回归方程类型?并求出回归方程(
哪一个适合作为每天净利润的回归方程类型?并求出回归方程(![]() ,
,![]() ,
,![]() ,
,![]() 精确到
精确到![]() );
);

(Ⅱ)超市为了刺激周一消费,拟在周一开展使用支付宝和微信支付随机抽奖活动,总奖金7万元.根据市场调查,抽奖活动能使使用支付宝和微信支付消费人数增加6千人,7千人,8千人,9千人的概率依次为![]() ,
,![]() ,
,![]() ,
,![]() .试决策超市是否有必要开展抽奖活动?
.试决策超市是否有必要开展抽奖活动?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中,随机抽取100名,按年龄(单位:岁)进行统计的频率分布直方图如图:

(1)根据频率分布直方图,分别求出样本的平均数(同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位);
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加华为手机宣传活动,现从这20人中,随机选取2人各赠送一部华为手机,求这2名市民年龄都在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)设集合C={x|m+1<x<2m-1},若B∩C=C,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com