
已知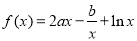 在
在 与
与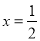 处都取得极值.
处都取得极值.
(1)求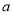 ,
,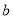 的值;
的值;
(2)设函数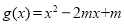 ,若对任意的
,若对任意的 ,总存在
,总存在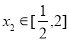 ,使得、
,使得、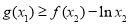 ,求实数
,求实数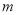 的取值范围.
的取值范围.
(1)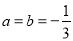 ;(2)
;(2)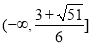 .
.
【解析】
试题分析:(1)根据条件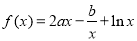 ,可得
,可得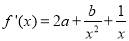 ,由
,由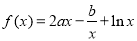 在
在 与
与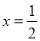 处都取得极值,可知
处都取得极值,可知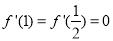 ,故可建立关于
,故可建立关于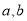 的二元一次方程组,从而解得
的二元一次方程组,从而解得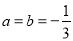 ,此时,需要代回检验
,此时,需要代回检验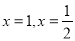 是否确实是
是否确实是 的极值点,经检验
的极值点,经检验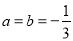 符合题意,从而
符合题意,从而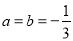 ;(2)由(1)可得由(1)知:函数
;(2)由(1)可得由(1)知:函数 在
在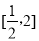 上递减,
上递减,
∴ 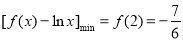 ,因此问题就等价于求使当
,因此问题就等价于求使当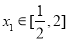 时,
时,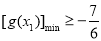 恒成立的
恒成立的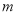 的取值范围,而二次函数
的取值范围,而二次函数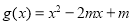 图像的对称轴是
图像的对称轴是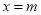 ,因此需对
,因此需对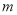 的取值作出以下三种情况的分类讨论:①:
的取值作出以下三种情况的分类讨论:①: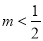 ;②:
;②: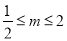 ;③
;③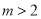 ,分别用含
,分别用含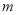 的代数式表示上述三种情况下
的代数式表示上述三种情况下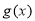 的最小值表示出来,从而可以建立关于
的最小值表示出来,从而可以建立关于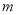 的不等式,进而求得
的不等式,进而求得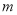 的取值范围为
的取值范围为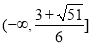 .
.
试题解析:(1)∵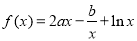 ,∴
,∴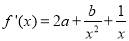 . 1分
. 1分
∵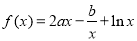 在
在 与
与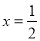 处都取得极值,
处都取得极值,
∴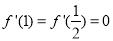 ,∴
,∴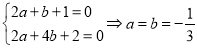 4分
4分
经检验,当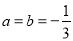 时,
时,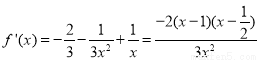 ,
,
∴函数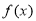 在
在 与
与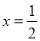 处都取得极值,∴
处都取得极值,∴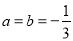 6分;
6分;
(2)由(1)知:函数 在
在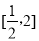 上递减,
上递减,
∴ 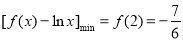 8分,
8分,
又 ∵函数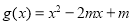 图象的对称轴是
图象的对称轴是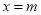 ,
,
①:当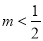 时:
时: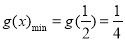 ,显然有
,显然有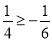 成立, ∴
成立, ∴ 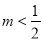 .
.
②:当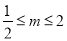 时:
时: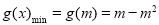 ,∴
,∴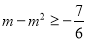 , 解得:
, 解得: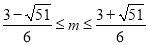 ,
,
又∵ 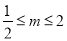 ,∴
,∴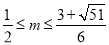 .
.
③:当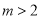 时:
时: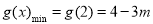 ,∴
,∴ 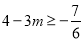 , ∴
, ∴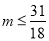 , 又
, 又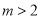 ,∴
,∴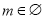
综上所述: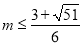 12分,
12分,
∴实数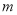 的取值范围为
的取值范围为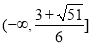 13分.
13分.
考点:1.导数的运用;2.二次函数与恒成立问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届湖北省武汉市高三9月调考文科数学试卷(解析版) 题型:选择题
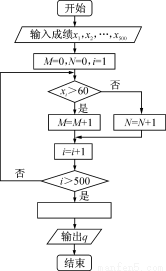
右图是计算某年级500名学生期末考试(满分为100分)及格率 的程序框图,则图中空白框内应填入( )
的程序框图,则图中空白框内应填入( )
A.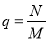 B.
B.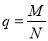 C.
C.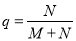 D.
D.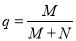
查看答案和解析>>
科目:高中数学 来源:2015届湖北省咸宁市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
不等式 的解集是( )
的解集是( )
A.(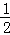 ,+
,+ )
)
B.(3,+ )
)
C.(﹣ ,﹣3)∪(4,+
,﹣3)∪(4,+ )
)
D.(﹣ ,﹣3)∪(
,﹣3)∪(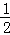 ,+
,+ )
)
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二5月月考理科数学试卷(解析版) 题型:填空题
如图所示,在半径为 的⊙O中,弦AB,CD相交于点P. PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
的⊙O中,弦AB,CD相交于点P. PA=PB=2,PD=1,则圆心O到弦CD的距离为________.

查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二5月月考文科数学试卷(解析版) 题型:填空题
两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数1,5,12,22, ,被称为五角形数,其中第1个五角形数记作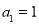 ,第2个五角形数记作
,第2个五角形数记作 ,第3个五角形数记作
,第3个五角形数记作 ,第4个五角形数记作
,第4个五角形数记作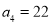 , ,若按此规律继续下去,则
, ,若按此规律继续下去,则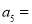 ,若
,若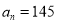 ,则
,则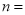 .
.

1 5 12 22
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设某几何体的三视图如图(尺寸的长度单位为m)则该几何体的体积为 _________ m3.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com