
分析 (1)根据题意f(x)图象的截距求出b3,由二次函数的最值和条件列出方程,利用等比中项的性质化简后,列出方程求出a6;
(2)由等差数列的性质、二次函数的性质化简条件,求出等比数列{bn}的公比,由等比数列的通项公式求出 数列{bn}的通项公式;
(3)由(1)和条件求出公差,由等差数列的通项公式求出an,代入 $\frac{1}{{a}_{n}{a}_{n+1}}$化简后,利用裂项相消法求出数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和.
解答 解:(1)∵函数f(x)=b1x2+b2x+b3的图象在y轴上的截距为-4,
∴b3=-4,
∵f(x)的最大值为a6-$\frac{7}{2}$,
∴当x=$-\frac{{b}_{2}}{2{b}_{1}}$时,f(x)取得最大值是a6-$\frac{7}{2}$,
即$\frac{4{b}_{1}{b}_{3}-{{b}_{2}}^{2}}{4{b}_{1}}$=b3-$\frac{{{b}_{2}}^{2}}{4{b}_{1}}$=a6-$\frac{7}{2}$,
∵{bn}是等比数列,∴${{b}_{2}}^{2}={b}_{1}{b}_{3}$,
代入上式得,-4+1=a6-$\frac{7}{2}$,解得a6=$\frac{1}{2}$;
(I2)∵数列{an}是公差d不为零的等差数列,
∴a2+a8=2a5,且a3+a11=2a7,
则 f(a2+a8)=f(a3+a11)为f(2a5)=f(2a7),
由(1)可得,$\frac{1}{2}$(2a5+2a7)=$-\frac{{b}_{2}}{2{b}_{1}}$,
∴a5+a7=$-\frac{{b}_{2}}{2{b}_{1}}$,即$-\frac{{b}_{2}}{2{b}_{1}}$=2a6=1,得$\frac{{b}_{2}}{{b}_{1}}$=-2
则数列{bn}的公比q=$\frac{{b}_{2}}{{b}_{1}}$=-2,
∴bn=b3•qn-3=-4×(-2)n-3=-(-2)n-1;
(3)由a2=-$\frac{7}{2}$,a6=$\frac{1}{2}$得,公差d=$\frac{{a}_{6}-{a}_{2}}{4}$=1,
∴an=a2+(n-2)d=-$\frac{7}{2}$+n-2=n-$\frac{11}{2}$=$\frac{2n-11}{2}$,
则$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{4}{(2n-11)(2n-9)}$=2($\frac{1}{2n-11}-\frac{1}{2n-9}$),
∴数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和:
Tn=2[($\frac{1}{-9}-\frac{1}{-7}$)+($\frac{1}{-7}-\frac{1}{-5}$)+…+($\frac{1}{2n-11}-\frac{1}{2n-9}$)]
=2(-$\frac{1}{9}$-$\frac{1}{2n-9}$ )=$\frac{-4n}{9(2n-9)}$.
点评 本题考查了等差数列的性质、通项公式,等比数列的通项公式,二次函数的图象与性质,以及裂项相消法求数列的前n项和,考查方程思想,化简、变形能力.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {2,4,5,6,7,8} | C. | {5,6,7} | D. | {4,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
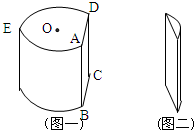 如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.
如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com