
分析 (1)利用递推关系、猜想此数列为等差数列,验证成立即可.
(2)利用等比数列的求和公式即可得出.
解答 解:(1)${S_{2n}}=2{a_n}^2+{a_n}$,则${S_2}={a_1}+{a_2}=2a_1^2+{a_1}$,又a1=1,得a2=2,
猜想数列{an}为等差数列,公差d=a2-a1=1,可得数列{an}的通项公式为an=n.
验证:左边=S2n=$\frac{2n(1+2n)}{2}$=2n2+n=右边.
∴猜想an=n正确.
(2)${b_n}={2^{a_n}}={2^n}$,
∴数列{b2n+1}是首项为2,公比为4的等比数列,
∴${b_1}+{b_3}+{b_5}+…+{b_{2n+1}}=\frac{2}{3}({{4^{n+1}}-1})$.
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y=x2-4x+3 | … | … |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
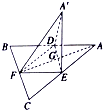 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )| A. | ① | B. | ①② | C. | ①②③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=P⊆N | B. | N=P⊆M | C. | M=N⊆P | D. | M=P=N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com