
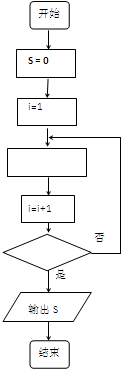
 根据下面的要求,求S=1+2+┅+100值.
根据下面的要求,求S=1+2+┅+100值.分析 (Ⅰ)分析题目中的要求,发现这是一个累加型的问题,可用循环结构来实现,在编写算法的过程中要注意,累加的初始值为0,累加值每一次增加1,退出循环的条件是i>100,把握住以上要点不难得到答案;
(Ⅱ)利用等差数列的求和公式即可得解.
解答 解:(Ⅰ)S=S+i________(3分)
i>100?-----(6分)
(Ⅱ)S=1+2+┅+100=$\frac{(1+100)×100}{2}=5050$----(12分)
点评 本题考查了程序框图,可利用循环语句来实现数值的累加(乘)常分如下步骤:①观察S的表达式分析,循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值,累加器的初值为0,累乘器的初值为1,环变量的初值同累加(乘)第一项的相关初值④在循环体中要先计算累加(乘)值,如果累加(乘)值比较简单可以省略此步,累加(乘),给循环变量加步长⑤输出累加(乘)值.本题属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com