
 如图,双曲线经过正六边形的四个顶点,且正六边形的另两个顶点A、B分别双曲线的两个焦点,则该双曲线的离心率为$\sqrt{3}+1$.
如图,双曲线经过正六边形的四个顶点,且正六边形的另两个顶点A、B分别双曲线的两个焦点,则该双曲线的离心率为$\sqrt{3}+1$. 分析 设正六边形的边长为2,画出图象做出辅助线,由正六边形的性质、双曲线的定义求出a和c,即可求出该双曲线的离心率的值.
解答 解:设正六边形的边长为2,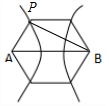 如图所示:
如图所示:
连接AB、AP、PB,
由正六边形的性质可得,AB=4,AP⊥BP,∠PAB=60°,
在RT△ABP中,PA=2,PB=2$\sqrt{3}$,
由双曲线的定义知,2c=AB=4,则C=2,
2a=PA+PB=2(1+$\sqrt{3}$),则a=1+$\sqrt{3}$,
所以该双曲线的离心率e=$\frac{c}{a}$=$\sqrt{3}+1$,
故答案为:$\sqrt{3}+1$.
点评 本题考查了双曲线的定义以及性质,正六边形的性质的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | (1,2) | C. | $({\frac{{2\sqrt{3}}}{3},+∞})$ | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABDC是圆O的内接四边形,B,D是圆O上的动点,AD与BC交于F,圆O的切线CE(C为切点)与线段AB的延长线交于E,∠BCD=∠CBD.
如图,已知四边形ABDC是圆O的内接四边形,B,D是圆O上的动点,AD与BC交于F,圆O的切线CE(C为切点)与线段AB的延长线交于E,∠BCD=∠CBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆短轴的两个端点和两个焦点所组成的四边形为正方形,且椭圆过点(-1,$\frac{\sqrt{2}}{2}$).
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆短轴的两个端点和两个焦点所组成的四边形为正方形,且椭圆过点(-1,$\frac{\sqrt{2}}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com