
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | (1,2) | C. | $({\frac{{2\sqrt{3}}}{3},+∞})$ | D. | (2,+∞) |
分析 过左焦点且倾斜角为30°直线与右支交于点A,即$\frac{b}{a}$>tan30°=$\frac{\sqrt{3}}{3}$,即b>$\frac{\sqrt{3}}{3}$a,c>$\frac{2\sqrt{3}}{3}$a,离心率公式e=$\frac{c}{a}$>$\frac{2\sqrt{3}}{3}$,求出离心率的范围,最后根据双曲线的离心率大于1,综合可得e的范围.
解答 解:过左焦点且倾斜角为30°直线与右支交于点A,即$\frac{b}{a}$>tan30°=$\frac{\sqrt{3}}{3}$,
∴b>$\frac{\sqrt{3}}{3}$a,
∵b=$\sqrt{{c}^{2}-{a}^{2}}$,
∴$\sqrt{{c}^{2}-{a}^{2}}$>$\frac{\sqrt{3}}{3}$a,
整理得:c>$\frac{2\sqrt{3}}{3}$a,
∴e=$\frac{c}{a}$>$\frac{2\sqrt{3}}{3}$,
∴e的范围是($\frac{2\sqrt{3}}{3}$,+∞)
故选C.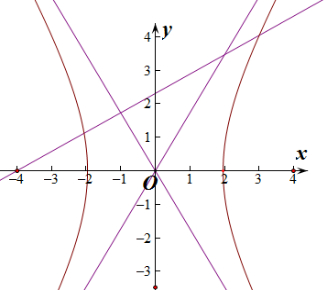
点评 本题考查双曲线的简单性质,考查直线与双曲线的位置关系,考查数形结合思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (-2,2) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=x0,g(x)=13x | ||
| C. | f(x)=3x,g(x)=($\frac{1}{3}$)-x | D. | f(x)=x-1,g(x)=$\frac{{x}^{2}-1}{x+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}π$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=($\frac{1}{3}$)|x| | C. | f(x)=sinx-x | D. | f(x)=$\frac{lnx}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com