
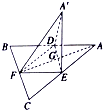
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )| A. | ① | B. | ①② | C. | ①②③ | D. | ②③ |
分析 对于①,根据面A′FG⊥面ABC,可得BC⊥FA′,又BC∥DE,则FA'⊥DE;对于②,根据BC∥DE,结合线面平行的判定定理得BC∥平面A'DE;对于③当面A′DE⊥面ABC时,三棱锥A′-FDE的体积达到最大,符合条件.
解答 解:①由已知可得面A′FG⊥面ABC,∴BC⊥FA′,又BC∥DE,∴FA'⊥DE;
②由BC∥DE,根据线面平行的判定定理可得BC∥平面A′DE;
③当面A′DE⊥面ABC时,三棱锥A′-FDE的体积达到最大.
∴正确命题的序号是①②③.
故选:C.
点评 本题主要考查了直线与平面平行的判定,以及三棱锥的体积的计算,考查对基础知识的综合应用能力和基本定理的掌握能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
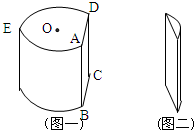 如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.
如图,点O为圆柱形木块底面的圆心,AD是底面圆的一条弦,优弧$\widehat{AED}$的长为底面圆的周长的$\frac{3}{4}$.过AD和母线AB的平面将木块剖开,得到截面ABCD,已知四边形ABCD的周长为40.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 随机数表法 | C. | 系统抽样法 | D. | 分层抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com