
分析 (1)利用有理指数幂的运算法则化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)原式=${({\frac{27}{8}})^{-\frac{2}{3}}}+{({\frac{1}{500}})^{-\frac{1}{2}}}-\frac{10}{{\sqrt{5}-2}}={({\frac{8}{27}})^{\frac{2}{3}}}+{500^{\frac{1}{2}}}-10({\sqrt{5}+2})$
=$\frac{4}{9}+10\sqrt{5}-10\sqrt{5}-20=-\frac{176}{9}$.
(2)原式=$[{1-2{{log}_6}3+{{({{{log}_6}3})}^2}+{{log}_6}\frac{6}{3}•{{log}_6}({6×3})}]÷{log_6}4$
=$[{1-2{{log}_6}3+{{({{{log}_6}3})}^2}+({1-{{log}_6}3})({1+{{log}_6}3})}]÷{log_6}4$
═$[{1-2{{log}_6}3+{{({{{log}_6}3})}^2}+1-{{({{{log}_6}3})}^2}}]÷{log_6}4=\frac{{21-{{log}_6}3}}{{2{{log}_6}2}}$
=$\frac{lo{g}_{6}6-lo{g}_{6}3}{2lo{g}_{6}2}$=$\frac{1}{2}$.
点评 本题考查有理指数幂以及对数运算法则的应用,考查计算能力.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
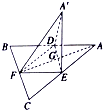 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是( )| A. | ① | B. | ①② | C. | ①②③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,AB⊥BC,CD=1,BC=4,AB=PA=PD=3,E为线段AB上一点,AE=$\frac{1}{2}$BE,F为PD的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,AB⊥BC,CD=1,BC=4,AB=PA=PD=3,E为线段AB上一点,AE=$\frac{1}{2}$BE,F为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com